Extremes, the largest and smallest values \u200b\u200bof functions. Local extrema of functions

28.09.2019

The extremum point of a function is the point in the domain of the function at which the value of the function takes a minimum or maximum value. The values \u200b\u200bof the function at these points are called the extrema (minimum and maximum) of the function.

Definition. Point x1 function definition areas f(x) is called function maximum point if the value of the function at this point is greater than the values \u200b\u200bof the function at points sufficiently close to it located to the right and left of it (i.e., the inequality f(x0 ) > f(x0 + Δ x) x1 maximum.

Definition. Point x2 function definition areas f(x) is called function minimum pointif the value of the function at this point is less than the values \u200b\u200bof the function at points sufficiently close to it located to the right and left of it (i.e., the inequality f(x0 ) < f(x0 + Δ x) ) In this case, they say that the function has at x2 minimum.

Let's say point x1 - point of maximum function f(x) Then in the interval to x1 function increases , therefore, the derivative of the function is greater than zero ( f "(x)\u003e 0), and in the interval after x1 function decreases therefore and derivative function less than zero ( f "(x) < 0 ). Тогда в точке x1

Assume also that the point x2 is the minimum point of the function f(x) Then in the interval to x2 the function decreases, and the derivative of the function is less than zero ( f "(x) < 0 ), а в интервале после x2 the function increases, and the derivative of the function is greater than zero ( f "(x)\u003e 0). In this case also at x2 the derivative of the function is zero or does not exist.

Fermat's theorem (a necessary sign of the existence of an extremum of a function). If the point x0 - function extremum point f(x), then at this point the derivative of the function is equal to zero ( f "(x) \u003d 0) or does not exist.

Definition. Points at which the derivative of the function is zero or does not exist are called critical points .

Example 1 Consider the function.

At the point x \u003d 0, the derivative of the function is zero, therefore, the point x \u003d 0 is a critical point. However, as can be seen in the graph of the function, it increases in the entire domain of definition, therefore, the point x \u003d 0 is not the extremum point of this function.

Thus, the conditions that the derivative of a function at a point is zero or does not exist are necessary conditions for the extremum, but not sufficient, since other examples of functions for which these conditions are satisfied, but the function does not have an extremum at the corresponding point, can be cited. therefore need to have sufficient signs, allowing us to judge whether there is an extremum at a particular critical point and which one is the maximum or minimum.

Theorem (the first sufficient sign of the existence of an extremum of a function). Critical point x0 f(x), if, when passing through this point, the derivative of the function changes sign, moreover, if the sign changes from "plus" to "minus", then the maximum point, and if from "minus" to "plus", then the minimum point.

If near the point x0 , to the left and to the right of it, the derivative retains the sign, this means that the function either only decreases or only increases in some neighborhood of the point x0 . In this case, at the point x0 there is no extremum.

So, to determine the extremum points of a function, the following is required :

Find the derivative of the function.
Set the derivative to zero and determine the critical points.
Mentally or on paper, note the critical points on the numerical axis and determine the signs of the derivative function in the obtained intervals. If the sign of the derivative changes from "plus" to "minus", then the critical point is the maximum point, and if from "minus" to "plus", then the minimum point.
Calculate the value of the function at the points of extremum.

Example 2 Find function extrema .

Decision. Find the derivative of the function:

We equate the derivative to zero to find the critical points:

Since the denominator is not equal to zero for any x-value, then we equate the numerator to zero:

Got one critical point x \u003d 3. We define the sign of the derivative in the intervals delimited by this point:

in the range from minus infinity to 3 - minus sign, that is, the function decreases,

in the range from 3 to plus infinity - a plus sign, that is, the function increases.

That is, point x \u003d 3 is the minimum point.

Find the value of the function at the minimum point:

Thus, the extremum point of the function is found: (3; 0), and it is the minimum point.

Theorem (the second sufficient sign of the existence of an extremum of a function). Critical point x0 is the extremum point of the function f(x) if the second derivative of the function at this point is not equal to zero ( f ""(x) ≠ 0), and if the second derivative is greater than zero ( f ""(x)\u003e 0), then the maximum point, and if the second derivative is less than zero ( f ""(x) < 0 ), то точкой минимума.

Remark 1. If at a point x0 if the first and second derivatives vanish, then at this point it is impossible to judge the presence of an extremum based on the second sufficient criterion. In this case, you need to use the first sufficient sign of the extremum of the function.

Remark 2. The second sufficient criterion for the extremum of the function is not applicable even when the first derivative does not exist at the stationary point (then the second derivative does not exist). In this case, you must also use the first sufficient sign of the extremum of the function.

Local character of function extrema

From the above definitions it follows that the extremum of the function has a local character - this is the largest and smallest value of the function in comparison with the nearest values.

Suppose you consider your earnings in a one-year time span. If in May you earned 45,000 rubles, and in April 42,000 rubles and in June 39,000 rubles, then May earnings are the maximum of the earnings function compared to the nearest values. But in October, you earned 71,000 rubles, in September 75,000 rubles, and in November 74,000 rubles, so the October earnings are a minimum of the earnings function compared to the nearest values. And you can easily see that the maximum among the April-May-June values \u200b\u200bis less than the September-October-November minimum.

Generally speaking, in the interval, a function can have several extrema, and it may turn out that some minimum of the function is greater than some maximum. So, for the function shown in the figure above,.

That is, one should not think that the maximum and minimum of the function are, respectively, its largest and smallest values \u200b\u200bover the entire considered segment. At the maximum point, the function has the greatest value only in comparison with those values \u200b\u200bthat it has at all points close enough to the maximum point, and at the minimum point it has the smallest value only in comparison with those values \u200b\u200bthat it has at all points close enough to the minimum point.

Therefore, we can clarify the concept of extremum points of a function given above and call the minimum points the local minimum points, and the maximum points the local maximum points.

Looking for extrema of the function together

Example 3

Solution: The function is defined and continuous on the whole number line. Its derivative also exists on the whole number line. Therefore, in this case, only those at which, i.e. , where and. The critical points and divide the entire domain of the function into three intervals of monotony:. We choose one control point in each of them and find the sign of the derivative at this point.

For the interval, the control point can be: we find. Taking the point in the interval, we get, and taking the point in the interval, we have. So, in the intervals and, and in the interval. According to the first sufficient criterion for an extremum, there is no extremum at the point (since the derivative preserves the sign in the interval), and at the point the function has a minimum (since the derivative changes sign from minus to plus when crossing this point). Find the corresponding function values:, a. In the interval, the function decreases, since in this interval, and in the interval increases, since in this interval.

To clarify the construction of the graph, we find the points of intersection with the coordinate axes. When we obtain an equation whose roots and, i.e., two points (0; 0) and (4; 0) are found for the graph of the function. Using all the information received, we build a graph (see the beginning of the example).

Example 4Find the extrema of the function and plot it.

The domain of the function is the entire numerical line, except for the point, i.e. .

To reduce the study, you can take advantage of the fact that this function is even, since . Therefore, its graph is symmetrical about the axis Oy and the study can only be done for the interval.

We find the derivative and critical points of the function:

1) ;

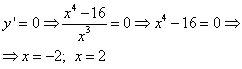2) ,

but the function suffers a break at this point, so it cannot be an extremum point.

Thus, a given function has two critical points: and. Given the parity of the function, we check only the point according to the second sufficient criterion of the extremum. To do this, find the second derivative and define its sign at: we get. Since and, it is the minimum point of the function, while .

To make a more complete picture of the function graph, we find out its behavior at the boundaries of the definition domain:

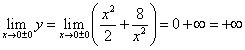
(here the symbol denotes the desire x to zero on the right, and x remains positive; similarly means striving x to zero on the left, and x remains negative). So, if, then. Next, we find

those. if, then.

The graph does not have points of intersection with the axes. The figure is at the beginning of the example.

We continue to search for extrema of the function together

Example 8Find the extrema of the function.

Decision. Find the domain of the function. Since the inequality must be fulfilled, we obtain from.

Find the first derivative of the function:

Find the critical points of the function.

Definition: The point x0 is called the point of local maximum (or minimum) of the function, if in some neighborhood of the point x0 the function takes the largest (or smallest) value, i.e. for all x from a neighborhood of x0, the condition f (x) f (x0) (or f (x) f (x0)) is satisfied.

The points of a local maximum or minimum are united by a common name - the points of the local extremum of a function.

Note that at points of a local extremum, a function reaches its greatest or smallest value only in a certain local region. There are cases when, according to the value maxaxmin.

A necessary sign of the existence of a local extremum of a function

Theorem . If the continuous function y \u003d f (x) has a local extremum at x0, then at this point the first derivative either vanishes or does not exist, i.e. a local extremum takes place at critical points of the first kind.

At the points of the local extremum, either the tangent is parallel to the 0x axis, or there are two tangents (see figure). Note that critical points are a necessary but insufficient condition for a local extremum. A local extremum occurs only at critical points of the first kind, but not at all critical points there is a local extremum.

For example: a cubic parabola y \u003d x3, has a critical point x0 \u003d 0, in which the derivative y / (0) \u003d 0, but the critical point x0 \u003d 0 is not an extremum point, but an inflection point takes place in it (see below).

A sufficient sign of the existence of a local extremum of a function

Theorem . If, when passing the argument through a critical point of the first kind, from left to right the first derivative y / (x)

changes sign from “+” to “-”, then the continuous function y (x) at this critical point has a local maximum;

changes sign from “-” to “+”, then the continuous function y (x) has a local minimum at this critical point

does not change sign, then at this critical point there is no local extremum, here there is an inflection point.

For a local maximum, the region of increasing function (y / 0) is replaced by the region of decreasing function (y / 0). For a local minimum, the region of decreasing function (y / 0) is replaced by the region of increasing function (y / 0).

Example: Investigate the function y \u003d x3 + 9x2 + 15x - 9 for monotony, extremum and plot the function.

We find critical points of the first kind by determining the derivative (y /) and equating it to zero: y / \u003d 3x2 + 18x + 15 \u003d 3 (x2 + 6x + 5) \u003d 0

We solve the quadratic trinomial using the discriminant:

x2 + 6x + 5 \u003d 0 (a \u003d 1, b \u003d 6, c \u003d 5) D \u003d, x1k \u003d -5, x2k \u003d -1.

2) We divide the numerical axis by critical points into 3 regions and define the signs of the derivative (y /) in them. Using these signs, we find the sections of monotonicity (increase and decrease) of the functions, and by changing the signs we determine the points of local extremum (maximum and minimum).

The research results will be presented in the form of a table from which the following conclusions can be drawn:

1. On the interval y / (- 10) 0, the function increases monotonically (the sign of the derivative y was estimated from the control point x \u003d -10 taken in this interval);
2. On the interval (-5; -1) y / (- 2) 0, the function decreases monotonically (the sign of the derivative y was estimated from the control point x \u003d -2 taken in this interval);
3. On the interval y / (0) 0, the function monotonically increases (the sign of the derivative y was estimated from the control point x \u003d 0 taken in this interval);
4. When passing through the critical point x1k \u003d -5, the derivative changes sign from "+" to "-", therefore this point is a local maximum point
(ymax (-5) \u003d (-5) 3 + 9 (-5) 2 +15 (-5) -9 \u003d -125 + 225 - 75 - 9 \u003d 16);
5. When passing through the critical point x2k \u003d -1, the derivative changes sign from "-" to "+", therefore this point is a local minimum point
(ymin (-1) \u003d -1 + 9 - 15 - 9 \u003d - 16).

x -5 (-5; -1) -1

3) We will construct the graph based on the results of the study with the use of additional calculations of the values \u200b\u200bof the function at the control points:

construct a rectangular coordinate system Ohu;

show the coordinates of the maximum point (-5; 16) and the minimum (-1; -16);

to refine the graph, we calculate the value of the function at the control points, choosing them to the left and to the right of the maximum and minimum points and inside the middle interval, for example: y (-6) \u003d (- 6) 3 +9 (-6) 2 + 15 (-6 ) -9 \u003d 9; y (-3) \u003d (- 3) 3 + 9 (-3) 2 + 15 (-3) -9 \u003d 0;

y (0) \u003d -9 (-6; 9); (-3; 0) and (0; -9) - calculated control points that we put to plot the graph;

we show the graph in the form of a curve with a bulge up at the maximum point and a bulge down at the minimum point and passing through the calculated control points.

For the function f (x) of many variables, the point x is a vector, f '(x) is the vector of the first derivatives (gradient) of the function f (x), f' '(x) is the symmetric matrix of the second partial derivatives (Hessian-Hessian matrix) function f (x).
For a function of many variables, optimality conditions are formulated as follows.
A necessary condition for local optimality. Let f (x) be differentiable at the point x * R n. If x * is the point of local extremum, then f ’(x *) \u003d 0.
As before, points that are solutions of a system of equations are called stationary. The character of the stationary point x * is associated with the sign-definiteness of the Hessian matrix f ′ ′ (x).
The sign-definiteness of the matrix A depends on the signs of the quadratic form Q (α) \u003d< α A, α > for all nonzero α∈R n.
Hereinafter through denotes the scalar product of the vectors x and y. A-priory,

A matrix A is positive (non-negative) definite if Q (α)\u003e 0 (Q (α) ≥0) for all nonzero α∈R n; negative (non-positive) definite if Q (α)<0 (Q(α)≤0) при всех ненулевых α∈R n ; неопределенной, если Q(α)>0 for some nonzero α∈R n and Q (α)<0 для остальных ненулевых α∈R n .
A sufficient condition for local optimality. Let f (x) be twice differentiable at the point x * R n, with f ’(x *) \u003d 0, i.e. x * is the stationary point. Then, if the matrix f ′ ′ (x *) is positive (negative) definite, then x * is the point of local minimum (maximum); if the matrix f ′ ′ (x *) is indefinite, then x * is a saddle point.
If the matrix f ′ ′ (x *) is non-negative (non-positive) definite, then to determine the nature of the stationary point x *, an investigation of higher-order derivatives is required.
To check the sign-definiteness of the matrix, as a rule, the Sylvester criterion is used. According to this criterion, a symmetric matrix A is positive definite if and only if all of its angular minors are positive. In this case, the determinant of a matrix constructed from the elements of matrix A standing at the intersection of rows and columns with the same (and first) numbers is called the angular minor of matrix A. To check the symmetric matrix A for negative definiteness, we need to check the matrix (−A) for positive definiteness.
So, the algorithm for determining the points of local extrema of the function of many variables is as follows.
1. Find f ′ (x).
2. The system is being solved

As a result, the stationary points x i are calculated.
3. There is f ′ ′ (x), it is assumed i \u003d 1.
4. There is f ′ ′ (x i)
5. The angular minors of the matrix f ′ ′ (x i) are calculated. If not all angular minors are nonzero, then to determine the nature of the stationary point x i, a study of higher-order derivatives is required. In this case, the transition to paragraph 8.
Otherwise, go to step 6.
6. The signs of the angular minors f ′ ′ (x i) are analyzed. If f ′ ′ (x i) is positive definite, then x i is a local minimum point. In this case, the transition to paragraph 8.
Otherwise, go to paragraph 7.
7. The angular minors of the matrix -f ′ ′ (x i) are calculated and their signs are analyzed.
If -f ′ ′ (x i) - is positive definite, then f ′ ′ (x i) is negative definite and x i is a local maximum point.
Otherwise, f ′ ′ (x i) is undefined and x i is a saddle point.
8. The condition for determining the nature of all stationary points i \u003d N is verified.
If it is executed, then the calculations are completed.
If the condition is not fulfilled, then i \u003d i + 1 is assumed and the transition to step 4 is carried out.

Example No. 1. Determine the points of local extrema of the function f (x) \u003d x 1 3 - 2x 1 x 2 + x 2 2 - 3x 1 - 2x 2

Since all angular minors are nonzero, the character x 2 is determined using f ′ ′ (x).
Since the matrix f ′ ′ (x 2) is positive definite, then x 2 is a local minimum point.
Answer: the function f (x) \u003d x 1 3 - 2x 1 x 2 + x 2 2 - 3x 1 - 2x 2 has a local minimum at the point x \u003d (5/3; 8/3).

$ E \\ subset \\ mathbb (R) ^ (n) $. They say that $ f $ has local maximum at the point $ x_ (0) \\ in E $ if there exists a neighborhood $ U $ of the point $ x_ (0) $ such that for all $ x \\ in U $ the inequality $ f \\ left (x \\ right) \\ leqslant f \\ left (x_ (0) \\ right) $.

The local maximum is called strict if the neighborhood $ U $ can be chosen so that for all $ x \\ in U $ other than $ x_ (0) $, there is $ f \\ left (x \\ right)< f\left(x_{0}\right)$.

Definition
Let $ f $ be a real function on the open set $ E \\ subset \\ mathbb (R) ^ (n) $. They say that $ f $ has local minimum at the point $ x_ (0) \\ in E $ if there exists a neighborhood $ U $ of the point $ x_ (0) $ such that for all $ x \\ in U $ the inequality $ f \\ left (x \\ right) \\ geqslant f \\ left (x_ (0) \\ right) $.

A local minimum is called strict if the neighborhood $ U $ can be chosen so that for all $ x \\ in U $ other than $ x_ (0) $, there is $ f \\ left (x \\ right)\u003e f \\ left (x_ ( 0) \\ right) $.

Local extremum combines the concepts of a local minimum and a local maximum.

Theorem (a necessary condition for the extremum of a differentiable function)
Let $ f $ be a real function on the open set $ E \\ subset \\ mathbb (R) ^ (n) $. If at the point $ x_ (0) \\ in E $ the function $ f $ has a local extremum at this point, then $$ \\ text (d) f \\ left (x_ (0) \\ right) \u003d 0. $$ Equality to zero differential is equivalent to the fact that all are equal to zero, i.e. $$ \\ displaystyle \\ frac (\\ partial f) (\\ partial x_ (i)) \\ left (x_ (0) \\ right) \u003d 0. $$

In the one-dimensional case, this is -. We denote $ \\ phi \\ left (t \\ right) \u003d f \\ left (x_ (0) + th \\ right) $, where $ h $ is an arbitrary vector. The function $ \\ phi $ is defined for sufficiently small modulo values \u200b\u200bof $ t $. In addition, by, it is differentiable, and $ (\\ phi) ’\\ left (t \\ right) \u003d \\ text (d) f \\ left (x_ (0) + th \\ right) h $.
Let $ f $ have a local maximum at x $ 0 $. Therefore, the function $ \\ phi $ with $ t \u003d 0 $ has a local maximum and, by Fermat’s theorem, $ (\\ phi) ’\\ left (0 \\ right) \u003d 0 $.
So, we got that $ df \\ left (x_ (0) \\ right) \u003d 0 $, i.e. of the function $ f $ at the point $ x_ (0) $ is equal to zero on any vector $ h $.

Definition
Points at which the differential is zero, i.e. those in which all partial derivatives are equal to zero are called stationary. Critical points the functions $ f $ are those points at which $ f $ is not differentiable, or is equal to zero. If the point is stationary, then this does not yet follow that at this point the function has an extremum.

Example 1
Let $ f \\ left (x, y \\ right) \u003d x ^ (3) + y ^ (3) $. Then $ \\ displaystyle \\ frac (\\ partial f) (\\ partial x) \u003d 3 \\ cdot x ^ (2) $, $ \\ displaystyle \\ frac (\\ partial f) (\\ partial y) \u003d 3 \\ cdot y ^ (2 ) $, so $ \\ left (0,0 \\ right) $ is a stationary point, but at this point the function has no extremum. Indeed, $ f \\ left (0,0 \\ right) \u003d 0 $, but it is easy to see that in any neighborhood of the point $ \\ left (0,0 \\ right) $ the function takes both positive and negative values.

Example 2
For the function $ f \\ left (x, y \\ right) \u003d x ^ (2) - y ^ (2) $, the origin is a stationary point, but it is clear that there is no extremum at this point.

Theorem (sufficient condition for an extremum).
Let a function $ f $ be twice continuously differentiable on an open set $ E \\ subset \\ mathbb (R) ^ (n) $. Let $ x_ (0) \\ in E $ be a stationary point and $$ \\ displaystyle Q_ (x_ (0)) \\ left (h \\ right) \\ equiv \\ sum_ (i \u003d 1) ^ n \\ sum_ (j \u003d 1) ^ n \\ frac (\\ partial ^ (2) f) (\\ partial x_ (i) \\ partial x_ (j)) \\ left (x_ (0) \\ right) h ^ (i) h ^ (j). $$ Then

if $ Q_ (x_ (0)) $ -, then the function $ f $ at the point $ x_ (0) $ has a local extremum, namely, the minimum if the form is positive definite, and the maximum if the form is negative definite;
if the quadratic form $ Q_ (x_ (0)) $ is indefinite, then the function $ f $ at the point $ x_ (0) $ has no extremum.

We use the expansion according to the Taylor formula (12.7 p. 292). Given that the first-order partial derivatives at the point $ x_ (0) $ are equal to zero, we obtain $$ \\ displaystyle f \\ left (x_ (0) + h \\ right) −f \\ left (x_ (0) \\ right) \u003d \\ \\ left (x_ (0) + \\ theta h \\ right) h ^ (i) h ^ (j), $$ where $ 0<\theta<1$. Обозначим $\displaystyle a_{ij}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right)$. В силу теоремы Шварца (12.6 стр. 289-290) , $a_{ij}=a_{ji}$. Обозначим $$\displaystyle \alpha_{ij} \left(h\right)=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}+\theta h\right)−\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}} \left(x_{0}\right).$$ По предположению, все непрерывны и поэтому $$\lim_{h \rightarrow 0} \alpha_{ij} \left(h\right)=0. \left(1\right)$$ Получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left.$$ Обозначим $$\displaystyle \epsilon \left(h\right)=\frac{1}{|h|^{2}}\sum_{i=1}^n \sum_{j=1}^n \alpha_{ij} \left(h\right)h_{i}h_{j}.$$ Тогда $$|\epsilon \left(h\right)| \leq \sum_{i=1}^n \sum_{j=1}^n |\alpha_{ij} \left(h\right)|$$ и, в силу соотношения $\left(1\right)$, имеем $\epsilon \left(h\right) \rightarrow 0$ при $h \rightarrow 0$. Окончательно получаем $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right)=\frac{1}{2}\left. \left(2\right)$$ Предположим, что $Q_{x_{0}}$ – положительноопределенная форма. Согласно лемме о положительноопределённой квадратичной форме (12.8.1 стр. 295, Лемма 1) , существует такое положительное число $\lambda$, что $Q_{x_{0}} \left(h\right) \geqslant \lambda|h|^{2}$ при любом $h$. Поэтому $$\displaystyle f \left(x_{0}+h\right)−f \left(x_{0}\right) \geq \frac{1}{2}|h|^{2} \left(λ+\epsilon \left(h\right)\right).$$ Так как $\lambda>0 $, and $ \\ epsilon \\ left (h \\ right) \\ rightarrow 0 $ for $ h \\ rightarrow 0 $, then the right side will be positive for any vector $ h $ of sufficiently short length.
So, we have come to the conclusion that in some neighborhood of the point $ x_ (0) $ the inequality $ f \\ left (x \\ right)\u003e f \\ left (x_ (0) \\ right) $ holds if only $ x \\ neq x_ (0) $ (we set $ x \u003d x_ (0) + h $ \\ right). This means that at the point $ x_ (0) $ the function has a strict local minimum, and this proves the first part of our theorem.
Suppose now that $ Q_ (x_ (0)) $ is an indefinite form. Then there are vectors $ h_ (1) $, $ h_ (2) $ such that $ Q_ (x_ (0)) \\ left (h_ (1) \\ right) \u003d \\ lambda_ (1)\u003e 0 $, $ Q_ (x_ (0)) \\ left (h_ (2) \\ right) \u003d \\ lambda_ (2)<0$. В соотношении $\left(2\right)$ $h=th_{1}$ $t>0 $. Then we get $$ f \\ left (x_ (0) + th_ (1) \\ right) −f \\ left (x_ (0) \\ right) \u003d \\ frac (1) (2) \\ left [t ^ (2) \\ left [\\ lambda_ (1) + | h_ (1) | ^ (2) \\ epsilon \\ left (th_ (1) \\ right) \\ right]. $$ For sufficiently small $ t\u003e 0 $ the right side is positive. This means that in any neighborhood of the point $ x_ (0) $, the function $ f $ takes values \u200b\u200b$ f \\ left (x \\ right) $ greater than $ f \\ left (x_ (0) \\ right) $.
Similarly, we find that in any neighborhood of the point $ x_ (0) $, the function $ f $ takes values \u200b\u200bless than $ f \\ left (x_ (0) \\ right) $. This, together with the previous one, means that at the point $ x_ (0) $ the function $ f $ does not have an extremum.

We consider a special case of this theorem for the function $ f \\ left (x, y \\ right) $ of two variables defined in a neighborhood of the point $ \\ left (x_ (0), y_ (0) \\ right) $ and having continuous in this neighborhood partial derivatives of the first and second orders. Assume that $ \\ left (x_ (0), y_ (0) \\ right) $ is a stationary point, and denote $$ \\ displaystyle a_ (11) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x ^ (2)) \\ left (x_ (0), y_ (0) \\ right), a_ (12) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x \\ partial y) \\ left (x_ ( 0), y_ (0) \\ right), a_ (22) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial y ^ (2)) \\ left (x_ (0), y_ (0) \\ right ). $$ Then the previous theorem will take the following form.

Theorem
Let $ \\ Delta \u003d a_ (11) \\ cdot a_ (22) - a_ (12) ^ 2 $. Then:

if $ \\ Delta\u003e 0 $, then the function $ f $ has a local extremum at the point $ \\ left (x_ (0), y_ (0) \\ right) $, namely, the minimum if $ a_ (11)\u003e 0 $ , and maximum if $ a_ (11)<0$;
if $ \\ Delta<0$, то экстремума в точке $\left(x_{0},y_{0}\right)$ нет. Как и в одномерном случае, при $\Delta=0$ экстремум может быть, а может и не быть.

Examples of solving problems

The algorithm for finding the extremum of the function of many variables:

Find the stationary points;
We find the 2nd order differential at all stationary points
Using the sufficient condition for the extremum of the function of many variables, we consider the second-order differential at each stationary point

Examine the extremum function $ f \\ left (x, y \\ right) \u003d x ^ (3) + 8 \\ cdot y ^ (3) + 18 \\ cdot x - 30 \\ cdot y $.
Decision
Find the 1st order partial derivatives: $$ \\ displaystyle \\ frac (\\ partial f) (\\ partial x) \u003d 3 \\ cdot x ^ (2) - 6 \\ cdot y; $$ $$ \\ displaystyle \\ frac (\\ partial f) (\\ partial y) \u003d 24 \\ cdot y ^ (2) - 6 \\ cdot x. $$ Create and solve the system: $$ \\ displaystyle \\ begin (cases) \\ frac (\\ partial f) (\\ partial x) \u003d 0 \\\\\\ frac (\\ partial f) (\\ partial y) \u003d 0 \\ end (cases) \\ Rightarrow \\ begin (cases) 3 \\ cdot x ^ (2) - 6 \\ cdot y \u003d 0 \\\\ 24 \\ cdot y ^ (2) - 6 \\ cdot x \u003d 0 \\ end (cases) \\ Rightarrow \\ begin (cases) x ^ (2) - 2 \\ cdot y \u003d 0 \\\\ 4 \\ cdot y ^ (2) - x \u003d 0 \\ end (cases) $$ From the 2nd equation we express $ x \u003d 4 \\ cdot y ^ (2) $ - we substitute into the 1st equation: $$ \\ displaystyle \\ left (4 \\ cdot y ^ (2) \\ right ) ^ (2) -2 \\ cdot y \u003d 0 $$ $$ 16 \\ cdot y ^ (4) - 2 \\ cdot y \u003d 0 $$ $$ 8 \\ cdot y ^ (4) - y \u003d 0 $$ $$ y \\ left (8 \\ cdot y ^ (3) -1 \\ right) \u003d 0 $$ As a result, 2 stationary points were obtained:
1) $ y \u003d 0 \\ Rightarrow x \u003d 0, M_ (1) \u003d \\ left (0, 0 \\ right) $;
2) $ \\ displaystyle 8 \\ cdot y ^ (3) -1 \u003d 0 \\ Rightarrow y ^ (3) \u003d \\ frac (1) (8) \\ Rightarrow y \u003d \\ frac (1) (2) \\ Rightarrow x \u003d 1 , M_ (2) \u003d \\ left (\\ frac (1) (2), 1 \\ right) $
We verify that the sufficient condition for the extremum
$$ \\ displaystyle \\ frac (\\ partial ^ (2) f) (\\ partial x ^ (2)) \u003d 6 \\ cdot x; \\ frac (\\ partial ^ (2) f) (\\ partial x \\ partial y) \u003d - 6; \\ frac (\\ partial ^ (2) f) (\\ partial y ^ (2)) \u003d 48 \\ cdot y $$
1) For the point $ M_ (1) \u003d \\ left (0,0 \\ right) $:
$$ \\ displaystyle A_ (1) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x ^ (2)) \\ left (0,0 \\ right) \u003d 0; B_ (1) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x \\ partial y) \\ left (0,0 \\ right) \u003d - 6; C_ (1) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial y ^ (2)) \\ left (0,0 \\ right) \u003d 0; $$
$ A_ (1) \\ cdot B_ (1) - C_ (1) ^ (2) \u003d -36<0$ , значит, в точке $M_{1}$ нет экстремума.
2) For the point $ M_ (2) $:
$$ \\ displaystyle A_ (2) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x ^ (2)) \\ left (1, \\ frac (1) (2) \\ right) \u003d 6; B_ (2) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x \\ partial y) \\ left (1, \\ frac (1) (2) \\ right) \u003d - 6; C_ (2) \u003d \\ frac (\\ partial ^ (2) f) (\\ partial y ^ (2)) \\ left (1, \\ frac (1) (2) \\ right) \u003d 24; $$
$ A_ (2) \\ cdot B_ (2) - C_ (2) ^ (2) \u003d 108\u003e 0 $, which means that there is an extremum at the point $ M_ (2) $, and since $ A_ (2)\u003e 0 $, then this is the minimum.
Answer: The point $ \\ displaystyle M_ (2) \\ left (1, \\ frac (1) (2) \\ right) $ is the minimum point of the function $ f $.
Investigate the extremum function $ f \u003d y ^ (2) + 2 \\ cdot x \\ cdot y - 4 \\ cdot x - 2 \\ cdot y - 3 $.
Decision
Find the stationary points: $$ \\ displaystyle \\ frac (\\ partial f) (\\ partial x) \u003d 2 \\ cdot y - 4; $$ $$ \\ displaystyle \\ frac (\\ partial f) (\\ partial y) \u003d 2 \\ cdot y + 2 \\ cdot x - 2. $$
We compose and solve the system: $$ \\ displaystyle \\ begin (cases) \\ frac (\\ partial f) (\\ partial x) \u003d 0 \\\\\\ frac (\\ partial f) (\\ partial y) \u003d 0 \\ end (cases) \\ 1 \\ end (cases) \\ Rightarrow x \u003d -1 $$
$ M_ (0) \\ left (-1, 2 \\ right) $ is a stationary point.
Let us verify that the sufficient condition for the extremum is satisfied: $$ \\ displaystyle A \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x ^ (2)) \\ left (-1,2 \\ right) \u003d 0; B \u003d \\ frac (\\ partial ^ (2) f) (\\ partial x \\ partial y) \\ left (-1,2 \\ right) \u003d 2; C \u003d \\ frac (\\ partial ^ (2) f) (\\ partial y ^ (2)) \\ left (-1,2 \\ right) \u003d 2; $$
$ A \\ cdot B - C ^ (2) \u003d -4<0$ , значит, в точке $M_{0}$ нет экстремума.
Answer: extrema are absent.

Time Limit: 0

Navigation (job numbers only)

0 out of 4 tasks completed

Information

Take this test to test your knowledge on the topic just read, “Local extrema of functions of many variables.”

You have already passed the test before. You cannot start it again.

The test is loading ...

You must login or register in order to start the test.

You must complete the following tests to start this:

results

Correct answers: 0 from 4

Your time:

Time is over

You scored 0 out of 0 points (0)

Your result has been recorded in the leaderboard.

With the answer
With watch mark

Task 1 of 4

1 .

Number of points: 1

Investigate the $ f $ function at extremes: $ f \u003d e ^ (x + y) (x ^ (2) -2 \\ cdot y ^ (2)) $

Right

Wrong

Task 2 of 4

2 .
Number of points: 1
Is there an extremum for the function $ f \u003d 4 + \\ sqrt ((x ^ (2) + y ^ (2)) ^ (2)) $

An increment of a function is an increment of an argument that tends to zero. To find it, use the table of derivatives. For example, the derivative of the function y \u003d x3 will be equal to y ’\u003d x2.

Set this derivative to zero (in this case x2 \u003d 0).

Find the value of the given variable. These will be those values, with this derivative equal to 0. To do this, substitute arbitrary digits in the expression instead of x, at which the whole expression will become zero. For example:

2-2x2 \u003d 0
(1-x) (1 + x) \u003d 0
x1 \u003d 1, x2 \u003d -1

Put the obtained values \u200b\u200bon the coordinate line and calculate the sign of the derivative for each of the received. On the coordinate line points are marked that are taken as the origin. To calculate the value at intervals, substitute arbitrary values \u200b\u200bthat match the criteria. For example, for the previous function, before the interval -1, you can select the value -2. From -1 to 1, you can select 0, and for values \u200b\u200bgreater than 1, select 2. Substitute these figures in the derivative and find out the sign of the derivative. In this case, the derivative with x \u003d -2 will be -0.24, i.e. negatively and at this interval there will be a minus sign. If x \u003d 0, then the value will be 2, and a sign is put on this interval. If x \u003d 1, then the derivative will also be equal to -0.24 and put a minus.

If, when passing through a point on the coordinate line, the derivative changes its sign from minus to plus, then this is the minimum point, and if from plus to minus, then this is the maximum point.

samarapedsovet.ru