Bugun sinfda biz ko'rib chiqamiz qat'iy ketma-ketlik Va funktsiya chegarasining qat'iy ta'rifi, shuningdek, nazariy xarakterdagi dolzarb masalalarni yechishni o'rganadi. Maqola, birinchi navbatda, matematik tahlil nazariyasini o'rganishni boshlagan va ushbu bo'limni tushunishda qiyinchiliklarga duch kelgan tabiiy fanlar va muhandislik mutaxassisliklarining 1-kurs talabalari uchun mo'ljallangan. oliy matematika. Bundan tashqari, material o'rta maktab o'quvchilari uchun juda qulay.

Sayt mavjud bo'lgan yillar davomida menga taxminan quyidagi mazmundagi o'nlab xatlar keldi: "Men matematik tahlilni yaxshi tushunmayapman, nima qilishim kerak?", "Men matematikani umuman tushunmayman, men o'qishni tashlab ketish haqida o'ylash" va boshqalar. Darhaqiqat, birinchi mashg'ulotdan keyin talabalar guruhini tez-tez yupqalashtiradigan matandir. Nima uchun bu shunday? Chunki mavzu tasavvur qilib bo'lmaydigan darajada murakkabmi? Arzimaydi! Matematik tahlil nazariyasi o'ziga xos bo'lganidek qiyin emas. Va siz uni kimligi uchun qabul qilishingiz va sevishingiz kerak =)

Eng qiyin holatdan boshlaylik. Birinchi va eng muhimi, siz o'qishdan voz kechishingiz shart emas. To'g'ri tushuning, tashlab qo'ying, bu har doim o'z vaqtida amalga oshiriladi;-) Albatta, agar bir-ikki yil ichida siz tanlagan mutaxassisligingizdan kasal bo'lib qolsangiz, ha, bu haqda o'ylashingiz kerak. (va g'azablanmang!) faoliyatning o'zgarishi haqida. Ammo hozircha buni davom ettirishga arziydi. Iltimos, "Men hech narsani tushunmayapman" iborasini unuting - siz umuman hech narsani tushunmaysiz.

Agar nazariya yomon bo'lsa, nima qilish kerak? Aytgancha, bu nafaqat matematik tahlilga tegishli. Agar nazariya yomon bo'lsa, birinchi navbatda siz amaliyotga jiddiy e'tibor qaratishingiz kerak. Bunday holda, bir vaqtning o'zida ikkita strategik vazifa hal qilinadi:

– Birinchidan, nazariy bilimlarning salmoqli qismi amaliyot orqali yuzaga keldi. Va shuning uchun ko'p odamlar nazariyani ... orqali tushunishadi - bu to'g'ri! Yo'q, yo'q, siz bu haqda o'ylamaysiz =)

- Va, ikkinchidan, amaliy ko'nikmalar sizni imtihondan o'tkazishi mumkin, hattoki ... lekin bu qadar hayajonlanmaylik! Hamma narsa haqiqiy va hamma narsani juda qisqa vaqt ichida "ko'tarish" mumkin. Matematik tahlil - bu oliy matematikaning eng sevimli bo'limi, shuning uchun men sizga yordam qo'lini bermay qo'ya olmadim:

1-semestr boshida, odatda, ketma-ketlik chegaralari va funktsiyalar chegaralari qoplanadi. Bu nima ekanligini tushunmayapsizmi va ularni qanday hal qilishni bilmayapsizmi? Maqola bilan boshlang Funktsiya chegaralari, unda kontseptsiyaning o'zi "barmoqlarda" ko'rib chiqiladi va eng oddiy misollar tahlil qilinadi. Keyinchalik, mavzu bo'yicha boshqa darslar, jumladan, haqida dars bilan ishlang ketma-ketliklar ichida, Men aslida qat'iy ta'rifni ishlab chiqqanman.

Tengsizlik belgilari va moduldan tashqari qanday belgilarni bilasiz?

- uzun vertikal tayoq quyidagicha o'qiydi: "bunday", "bunday", "bunday" yoki "bunday", bizning holatlarimizda, aniqki, biz raqam haqida gapiramiz - shuning uchun "bunday";

– dan katta bo‘lgan barcha “en” uchun;

– modul belgisi masofani bildiradi, ya'ni. Ushbu yozuv bizga qiymatlar orasidagi masofa epsilondan kamroq ekanligini aytadi.

Xo'sh, bu halokatli qiyinmi? =)

Amaliyotni o'zlashtirgandan so'ng, sizni keyingi paragrafda ko'rishni orziqib kutaman:

Va aslida, keling, bir oz o'ylab ko'raylik - ketma-ketlikning qat'iy ta'rifini qanday shakllantirish kerak? ...Dunyoda birinchi bo‘lib aqlga kelgan narsa amaliy dars: "ketma-ketlik chegarasi - ketma-ketlik a'zolari cheksiz yaqinlashadigan son."

Mayli, yozamiz keyingi ketma-ketlik :

Buni tushunish qiyin emas keyingi ketma-ketlik –1 soniga cheksiz yaqinlik va juft sonli hadlar - "bir" ga.

Yoki ikkita chegara bormi? Ammo nega hech qanday ketma-ketlikda ulardan o'n yoki yigirmatasi bo'lishi mumkin emas? Siz bu yo'ldan uzoqqa borishingiz mumkin. Shu munosabat bilan, deb taxmin qilish mantiqan to'g'ri keladi agar ketma-ketlikning chegarasi bo'lsa, u yagonadir.

Eslatma : ketma-ketlikning chegarasi yo'q, lekin undan ikkita kichik ketma-ketlikni ajratish mumkin (yuqoriga qarang), ularning har biri o'z chegarasiga ega.

Shunday qilib, yuqoridagi ta'rif asossiz bo'lib chiqadi. Ha, u kabi holatlar uchun ishlaydi (amaliy misollarning soddalashtirilgan tushuntirishlarida men unchalik to'g'ri foydalanmadim), lekin endi biz qat'iy ta'rifni topishimiz kerak.

Ikkinchi urinish: "ketma-ketlik chegarasi - bu ketma-ketlikning BARCHA a'zolari yaqinlashadigan raqam, ehtimol ularning sonidan tashqari. final miqdorlar." Bu haqiqatga yaqinroq, ammo baribir to'liq aniq emas. Shunday qilib, masalan, ketma-ketlik atamalarning yarmi umuman nolga yaqinlashmaydi - ular shunchaki unga teng =) Aytgancha, "miltillovchi chiroq" odatda ikkita sobit qiymatni oladi.

Formulyatsiyani aniqlashtirish qiyin emas, lekin keyin yana bir savol tug'iladi: ta'rifni matematik belgilarda qanday yozish kerak? Ilmiy dunyo Vaziyatni hal qilgunimcha, men bu muammo bilan uzoq vaqt kurashdim mashhur maestro, bu mohiyatan klassik matematik tahlilni butun jiddiyligi bilan rasmiylashtirgan. Koshi jarrohlik amaliyotini taklif qildi atrof-muhit , bu nazariyani sezilarli darajada ilgari surdi.

Ba'zi bir nuqtani ko'rib chiqing va uning o'zboshimchalik bilan-atrof:

"Epsilon" qiymati har doim ijobiydir va bundan tashqari, uni o'zimiz tanlashga haqlimiz. Faraz qilaylik, bu mahallada ko'plab a'zolar bor (hammasi shart emas) ba'zi ketma-ketlik. Masalan, o'ninchi davr mahallada ekanligini qanday yozish kerak? Uning o'ng tomonida bo'lsin. Keyin nuqtalar orasidagi masofa va "epsilon" dan kam bo'lishi kerak: . Biroq, agar "x o'ninchi" "a" nuqtasining chap tomonida joylashgan bo'lsa, farq salbiy bo'ladi va shuning uchun unga belgi qo'shilishi kerak. modul: .

Ta'rif: agar raqam ketma-ketlikning chegarasi deyiladi har qanday uchun uning atrofi (oldindan tanlangan) BUNDAY natural son bor HAMMA Yuqori raqamlarga ega bo'lgan ketma-ketlik a'zolari mahalla ichida bo'ladi:

Yoki qisqasi: agar

Boshqacha qilib aytganda, “epsilon” qiymati qanchalik kichik bo'lmasin, ertami-kechmi ketma-ketlikning “cheksiz dumi” TO'LIMI shu mahallada bo'ladi.

Masalan, ketma-ketlikning "cheksiz dumi" nuqtaning har qanday o'zboshimchalik bilan kichik mahallasiga TO'LIMI kiradi. Demak, bu qiymat ta'rif bo'yicha ketma-ketlikning chegarasidir. Eslatib o'taman, chegarasi nolga teng bo'lgan ketma-ketlik chaqiriladi cheksiz kichik.

Shuni ta'kidlash kerakki, ketma-ketlik uchun endi "cheksiz dum" deyish mumkin emas. kirib keladi"- toq sonli a'zolar aslida nolga teng va "hech qaerga bormanglar" =) Shuning uchun ta'rifda "paydo bo'ladi" fe'li ishlatilgan. Va, albatta, bu kabi ketma-ketlik a'zolari ham "hech qaerga bormaydilar". Aytgancha, raqam uning chegarasi yoki yo'qligini tekshiring.

Endi biz ketma-ketlikning chegarasi yo'qligini ko'rsatamiz. Misol uchun, nuqta qo'shnisini ko'rib chiqing. Ma'lum bir mahallada BARCHA atamalar tugaydigan bunday raqam yo'qligi aniq - toq atamalar har doim "minus bir" ga "sakrab chiqadi". Xuddi shunday sababga ko'ra, nuqtada hech qanday chegara yo'q.

Keling, materialni amaliyot bilan birlashtiramiz:

1-misol

Ketma-ketlik chegarasi nolga teng ekanligini isbotlang. Nuqtaning istalgan kichik mahallasida ketma-ketlikning barcha a'zolariga kafolat beriladigan raqamni ko'rsating.

Eslatma : Ko'p ketma-ketliklar uchun kerakli natural son qiymatga bog'liq - shuning uchun yozuv .

Yechim: o'ylab ko'ring o'zboshimchalik bilan bormi raqam - shunday qilib, raqamlari yuqori bo'lgan HAMMA a'zolar shu mahallada bo'ladi:

Kerakli sonning mavjudligini ko'rsatish uchun uni orqali ifodalaymiz.

“en” ning istalgan qiymati uchun modul belgisi olib tashlanishi mumkin:

Biz sinfda takrorlagan tengsizliklar bilan "maktab" harakatlaridan foydalanamiz Chiziqli tengsizliklar Va Funktsiya domeni. Bunday holda, "epsilon" va "en" ijobiy bo'lishi muhim holat:

Chapdagi tabiiy sonlar va o'ng tomoni odatda kasr bo'lganligi sababli, uni yaxlitlash kerak:

Eslatma : ba'zan xavfsiz tomonda bo'lish uchun o'ngga birlik qo'shiladi, lekin aslida bu ortiqcha. Nisbatan aytganda, agar yaxlitlash orqali natijani zaiflashtirsak, unda eng yaqin mos raqam ("uch") asl tengsizlikni qondiradi.

Endi biz tengsizlikni ko'rib chiqamiz va dastlab nimani ko'rib chiqqanimizni eslaymiz o'zboshimchalik bilan-mahalla, ya'ni. "epsilon" ga teng bo'lishi mumkin har kim ijobiy raqam.

Xulosa: nuqtaning har qanday ixtiyoriy kichik -qo'shnisi uchun qiymat topildi . Shunday qilib, raqam ta'rifi bo'yicha ketma-ketlikning chegarasidir. Q.E.D.

Aytgancha, olingan natijadan tabiiy naqsh aniq ko'rinadi: mahalla qanchalik kichik bo'lsa, raqam shunchalik katta bo'ladi, shundan so'ng ketma-ketlikning HAMMA a'zolari shu mahallada bo'ladi. Ammo "epsilon" qanchalik kichik bo'lmasin, har doim ichkarida "cheksiz dum" bo'ladi va tashqarida - hatto katta bo'lsa ham, lekin final a'zolar soni.

Taassurotlaringiz qanday? =) Men bu biroz g'alati ekanligiga qo'shilaman. Lekin qat'iy! Iltimos, qayta o'qing va hamma narsani yana o'ylab ko'ring.

Keling, shunga o'xshash misolni ko'rib chiqaylik va boshqa texnik texnikalar bilan tanishamiz:

2-misol

Yechim: ketma-ketlikning ta'rifi bilan buni isbotlash kerak (baland ovozda ayting!!!).

Keling, ko'rib chiqaylik o'zboshimchalik bilan-punkt va chekning qo'shniligi; mavjudmi natural son - shundayki, barcha katta sonlar uchun quyidagi tengsizlik amal qiladi:

Bundaylarning mavjudligini ko'rsatish uchun siz "epsilon" orqali "en" ni ifodalashingiz kerak. Modul belgisi ostidagi ifodani soddalashtiramiz:

Modul minus belgisini yo'q qiladi:

Denominator har qanday "en" uchun ijobiydir, shuning uchun tayoqlarni olib tashlash mumkin:

Aralash:

Endi biz chiqarib olishimiz kerak kvadrat ildiz, lekin ushlash shundaki, ba'zi "epsilon" uchun o'ng tomon salbiy bo'ladi. Ushbu muammodan qochish uchun mustahkamlaymiz modul bo'yicha tengsizlik:

Nima uchun buni qilish mumkin? Agar nisbatan aytganda, shunday bo'lib chiqsa, u holda shart ham qondiriladi. Modul mumkin shunchaki oshiring kerakli raqam va bu bizga ham mos keladi! Taxminan aytganda, agar yuzinchi mos bo'lsa, ikki yuzinchi ham mos keladi! Ta'rifga ko'ra, siz ko'rsatishingiz kerak raqamning mavjudligi haqiqati(hech bo'lmaganda ba'zi), shundan keyin ketma-ketlikning barcha a'zolari -mahallada bo'ladi. Aytgancha, shuning uchun biz o'ng tomonni yuqoriga qarab yakuniy yaxlitlashdan qo'rqmaymiz.

Ildizni ajratib olish:

Va natijani aylantiring: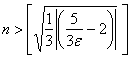

Xulosa: chunki "epsilon" qiymati o'zboshimchalik bilan tanlangan, keyin nuqtaning har qanday o'zboshimchalik bilan kichik qo'shnisi uchun qiymat topilgan. , shunday qilib, barcha katta raqamlar uchun tengsizlik o'rinli bo'ladi . Shunday qilib, ta'rifi bo'yicha. Q.E.D.

maslahat beraman ayniqsa tengsizliklarning kuchayishi va zaiflashishini tushunish matematik tahlilning tipik va juda keng tarqalgan usullaridir. Kuzatishingiz kerak bo'lgan yagona narsa - bu yoki boshqa harakatning to'g'riligi. Masalan, tengsizlik hech qanday sharoitda mumkin emas bo'shatish, ayirish, aytaylik, bir:

Shunga qaramay, shartli ravishda: agar raqam to'liq mos kelsa, avvalgisi endi mos kelmasligi mumkin.

Mustaqil yechim uchun quyidagi misol:

3-misol

Ketma-ketlik ta'rifidan foydalanib, buni isbotlang

Dars oxirida qisqacha yechim va javob.

Agar ketma-ketlik cheksiz katta, u holda chegaraning ta'rifi shunga o'xshash tarzda tuziladi: nuqta ketma-ketlikning chegarasi deb ataladi, agar mavjud bo'lsa, xohlaganingizcha katta soni, shunday son borki, barcha katta sonlar uchun tengsizlik qondiriladi. Raqam chaqiriladi "ortiqcha cheksizlik" nuqtasiga yaqinlik:

Boshqacha aytganda, nima bo'lishidan qat'iy nazar katta qiymat Nima bo'lishidan qat'iy nazar, ketma-ketlikning "cheksiz dumi" aniq nuqtaning qo'shnisiga kiradi va chap tomonda faqat cheklangan sonli atamalar qoladi.

Standart misol:

Va stenografiya: agar

Vaziyat uchun ta'rifni o'zingiz yozing. To'g'ri versiya dars oxirida.

Qo'lingizni olganingizdan keyin amaliy misollar Agar ketma-ketlik chegarasining ta'rifini aniqlagan bo'lsangiz, siz matematik tahlil bo'yicha adabiyotlarga va/yoki ma'ruza daftaringizga murojaat qilishingiz mumkin. Men Bohanning 1 jildini yuklab olishni tavsiya qilaman (oddiyroq - sirtqi talabalar uchun) va Fichtenholtz (batafsil va batafsil). Boshqa mualliflar qatorida men Piskunovni tavsiya qilaman, uning kursi texnik universitetlarga qaratilgan.

Ketma-ketlik chegarasi, ularning dalillari, oqibatlariga tegishli teoremalarni vijdonan o'rganishga harakat qiling. Dastlab, nazariya "bulutli" bo'lib tuyulishi mumkin, ammo bu normal holat - siz shunchaki ko'nikishingiz kerak. Va ko'pchilik buning ta'mini his qiladi!

Funksiya chegarasining qat'iy ta'rifi

Keling, xuddi shu narsadan boshlaylik - qanday shakllantirish kerak bu tushuncha? Funktsiya chegarasining og'zaki ta'rifi ancha sodda tarzda ifodalangan: "agar "x" ga moyil bo'lsa, son - bu funktsiyaning chegarasi. (chap va o'ng), mos keladigan funktsiya qiymatlari » (rasmga qarang). Hamma narsa normaldek tuyuladi, lekin so'zlar - so'zlar, ma'no - ma'no, piktogramma - bu belgi va qattiq matematik belgilar etarli emas. Va ikkinchi xatboshida biz ushbu masalani hal qilishning ikkita yondashuvi bilan tanishamiz.

Funktsiya ma'lum bir oraliqda aniqlansin, mumkin bo'lgan nuqtadan tashqari. O'quv adabiyotlarida u erda funktsiyasi umumiy qabul qilingan Yo'q belgilangan:

Bu tanlov ta'kidlaydi funksiya chegarasining mohiyati: "x" cheksiz yaqin yondashuvlar va funksiyaning mos qiymatlari cheksiz yaqin ga. Boshqacha qilib aytadigan bo'lsak, chegara tushunchasi nuqtalarga "aniq yondashuv" ni anglatmaydi, balki aniq cheksiz yaqinlik, funktsiyaning nuqtada aniqlangan yoki aniqlanmaganligi muhim emas.

Funktsiya chegarasining birinchi ta'rifi, ajablanarli emas, ikkita ketma-ketlik yordamida tuzilgan. Birinchidan, tushunchalar o'zaro bog'liq, ikkinchidan, funktsiyalar chegaralari odatda ketma-ketlik chegaralaridan keyin o'rganiladi.

Ketma-ketlikni ko'rib chiqing ball (chizmada emas), intervalga tegishli va dan farq qiladi, qaysi birlashadi ga. Keyin mos keladigan funktsiya qiymatlari ham a'zolari ordinata o'qida joylashgan sonli ketma-ketlikni hosil qiladi.

Geyne bo'yicha funksiya chegarasi har qanday uchun nuqtalar ketma-ketligi (tegishli va undan farqli) nuqtaga yaqinlashadigan , funktsiya qiymatlarining mos keladigan ketma-ketligi ga yaqinlashadi.

Eduard Geyne - nemis matematiki. ...Bunday o'ylashning hojati yo'q, Evropada faqat bitta gey bor - Gey-Lyusak =)

Limitning ikkinchi ta'rifi yaratildi... ha, ha, siz haqsiz. Ammo birinchi navbatda uning dizaynini tushunamiz. Nuqtaning o'zboshimchalik bilan qo'shniligini ko'rib chiqing ("qora" mahalla). Oldingi paragrafga asoslanib, yozuv shuni anglatadiki ba'zi qiymat funksiya "epsilon" mahallasida joylashgan.

Endi berilgan -mahallaga mos keladigan -mahallani topamiz (qora nuqtali chiziqlarni aqliy ravishda chapdan o'ngga, so'ngra yuqoridan pastga qarating). E'tibor bering, qiymat tanlangan kichikroq segmentning uzunligi bo'ylab, bu holda - qisqaroq chap segmentning uzunligi bo'ylab. Bundan tashqari, "malina" - nuqtaning qo'shnisi hatto qisqartirilishi mumkin, chunki quyidagi ta'rifda mavjudligi haqiqatining o'zi muhimdir bu mahalla. Va shunga o'xshab, belgi "delta" mahallasida ba'zi qiymatlar mavjudligini anglatadi.

Koshi funktsiyasi chegarasi: son funksiyaning nuqtadagi chegarasi deyiladi if har qanday uchun oldindan tanlangan Turar joy dahasi (siz xohlagancha kichik), mavjud- nuqta qo'shnisi, BUNDAY, bu: FAQAT qadriyatlar sifatida (tegishli) ushbu hududga kiritilgan: (qizil o'qlar)- SHUNDAN DARXOL mos funksiya qiymatlari qo'shni hududga kirishi kafolatlanadi: (ko'k o'qlar).

Men sizni ogohlantirishim kerakki, tushunarli bo'lishi uchun men biroz improvizatsiya qildim, shuning uchun ortiqcha ishlatmang =)

Qisqa yozuv: , agar

Ta'rifning mohiyati nimada? Majoziy ma'noda, qo'shnichilikni cheksiz qisqartirish orqali biz funktsiya qiymatlariga o'z chegarasigacha "hamrohlik qilamiz" va ularga boshqa joyga yaqinlashishga muqobil bo'lmaymiz. Juda g'ayrioddiy, lekin yana qat'iy! Fikrni to'liq tushunish uchun so'zlarni qayta o'qing.

! Diqqat: agar siz faqat shakllantirishingiz kerak bo'lsa Geyne ta'rifi yoki shunchaki Koshi ta'rifi iltimos unutmang muhim dastlabki mulohazalar: "Ma'lum bir oraliqda aniqlangan funktsiyani ko'rib chiqing, ehtimol nuqtadan tashqari". Men buni boshida bir marta aytdim va har safar takrorlamadim.

Matematik tahlilning tegishli teoremasiga ko'ra, Geyn va Koshi ta'riflari ekvivalentdir, ammo ikkinchi variant eng mashhurdir. (albatta!), bu "til chegarasi" deb ham ataladi:

4-misol

Limit ta'rifidan foydalanib, buni isbotlang

Yechim: funktsiya nuqtadan tashqari butun son chizig'ida aniqlanadi. Ta'rifdan foydalanib, biz berilgan nuqtada chegara mavjudligini isbotlaymiz.

Eslatma : "delta" mahallasining qiymati "epsilon" ga bog'liq, shuning uchun belgilash

Keling, ko'rib chiqaylik o'zboshimchalik bilan-atrof. Vazifa bu qiymatdan foydalanish yoki yo'qligini tekshirishdir mavjudmi-atrof, BUNDAY, bu tengsizlikdan tengsizlik kelib chiqadi .

deb faraz qilsak, oxirgi tengsizlikni o'zgartiramiz:
(kvadrat uch a’zoni kengaytirdi)

Xn - ketma-ketlikning elementlari yoki a'zolari, n - ketma-ketlikning a'zosi. Agar f(n) funksiya analitik, ya’ni formula bilan berilgan bo’lsa, xn=f(n) ketma-ketlik hadining formulasi deyiladi.

Agar har qanday e>0 uchun n=n(e) bo‘lsa, a soni ketma-ketlikning chegarasi (xn) deyiladi, undan boshlab |xn-a |

2-misol. 1-misol shartlarida a=1 soni oldingi misol ketma-ketligi chegarasi emasligini isbotlang. Yechim. Ketma-ketlikning umumiy atamasini yana soddalashtiring. e=1 ni oling (bu istalgan raqam >

Ketma-ketlik chegarasini to'g'ridan-to'g'ri hisoblash muammolari juda monotondir. Ularning barchasida n ga nisbatan ko‘phad munosabatlari yoki bu ko‘phadlarga nisbatan irratsional ifodalar mavjud. Yechishni boshlaganda, komponentni qavslar ichidan eng yuqori darajaga qo'ying (radikal belgi). Bu asl ifodaning soni uchun a^p, maxraj uchun esa b^q ko'paytmasining paydo bo'lishiga olib kelsin. Shubhasiz, qolgan barcha atamalar C/(n-k) ko'rinishga ega va n> sifatida nolga moyil bo'ladi.

Ketma-ketlik chegarasini hisoblashning birinchi usuli uning ta'rifiga asoslanadi. Ammo shuni esda tutish kerakki, u to'g'ridan-to'g'ri chegarani qidirish usullarini taqdim etmaydi, faqat har qanday a soni chegara ekanligini (yoki emasligini) isbotlashga imkon beradi. (3n^2-2n -1)/(n^2-n-2)) chegarasi a=3.Echim. Ta'rifni teskari tartibda qo'llash orqali isbotni bajaring. Ya'ni o'ngdan chapga. Avval xn.xn =(3n^2+4n+2)/(n^2+3n22)=((3n+1)(n+1))/(() formulasini soddalashtirish mumkinligini tekshiring. n+2) (n+1))=)=(3n+1)/(n+2) |(3n+1)/(n+2)-3|0 tengsizligini ko‘rib chiqsak, istalgan naturalni topishingiz mumkin. n e soni -2+ 5/e dan katta.

2-misol. 1-misol shartlarida a=1 soni oldingi misol ketma-ketligi chegarasi emasligini isbotlang. Yechim. Ketma-ketlikning umumiy atamasini yana soddalashtiring. e=1 ni oling (bu har qanday son >0) yakunlovchi tengsizlikni yozing umumiy ta'rif|(3n+1)/(n+2)-1|

Ketma-ketlik chegarasini to'g'ridan-to'g'ri hisoblash muammolari juda monotondir. Ularning barchasi n ga nisbatan ko‘phad munosabatlarini yoki bu ko‘phadlarga nisbatan irratsional ifodalarni o‘z ichiga oladi. Yechishni boshlaganda, komponentni qavslar ichidan eng yuqori darajaga qo'ying (radikal belgi). Bu asl ifodaning soni uchun a^p, maxraj uchun esa b^q ko'paytmasining paydo bo'lishiga olib kelsin. Shubhasiz, qolgan barcha shartlar C/(n-k) ko‘rinishga ega va n>k (n cheksizlikka intiladi) kabi nolga intiladi. Shundan so'ng, javobni yozing: 0, agar pq.

Ketma-ketlik chegarasini va cheksiz summalarni topishning noan'anaviy usulini ko'rsatamiz. Funktsional ketma-ketliklardan foydalanamiz (ularning funktsiya shartlari qandaydir (a,b) oraliqda aniqlanadi) 3-misol. 1+1/2 ko'rinishdagi yig'indini toping! +1/3! +…+1/n! +…=s .Echim. Har qanday raqam a^0=1. 1=exp(0) ni belgilang va funktsional ketma-ketlikni ko'rib chiqing (1+x+x^2/2! +x^3/3! +…+x^/n, n=0,1,2,..,n… . Легко заметить, что записанный полином совпадает с многочленом Тейлора по степеням x, который в данном случае совпадает с exp(x). Возьмите х=1. Тогдаexp(1)=e=1+1+1/2! +1/3! +…+1/n! +…=1+s. Ответ s=e-1.!}

Raqamlar ketma-ketligi chegarasi son fazosining elementlari ketma-ketligi chegarasi. Raqamli fazo - metrik fazo bo'lib, unda masofa elementlar orasidagi farq moduli sifatida aniqlanadi. Shuning uchun raqam chaqiriladi ketma-ketlikning chegarasi, agar har qanday uchun tengsizlikka bog'liq bo'lgan raqam mavjud bo'lsa.

Haqiqiy sonlar ketma-ketligining chegarasi tushunchasi juda sodda va vaziyatda tuzilgan murakkab sonlar ketma-ketlik chegarasining mavjudligi kompleks sonlarning haqiqiy va xayoliy qismlarining tegishli ketma-ketliklarining chegaralari mavjudligiga tengdir.

Limit (sonli ketma-ketlik) matematik analizning asosiy tushunchalaridan biridir. Har bir haqiqiy sonni yaqinlashishlar ketma-ketligining chegarasi sifatida ko'rsatish mumkin kerakli qiymat. Sanoq sistemasi bunday takomillashtirish ketma-ketligini ta'minlaydi. Irratsional butun sonlar yaqinlashishlarning davriy ketma-ketligi bilan, irratsional sonlar esa davriy bo‘lmagan yaqinlashishlar ketma-ketligi bilan tavsiflanadi.

Belgilari cheklangan sonli raqamlarni ifodalash qo'llaniladigan raqamli usullarda yaqinlashish tizimini tanlash alohida rol o'ynaydi. Taxminlovchi tizim sifatining mezoni yaqinlashuv tezligidir. Shu munosabat bilan raqamlarni davomli kasrlar shaklida ifodalash samarali bo'lib chiqadi.

Ta'rif

Raqam chaqiriladi raqamlar ketma-ketligi chegarasi, agar ketma-ketlik cheksiz kichik bo'lsa, ya'ni uning barcha elementlari, ma'lum biridan boshlab, mutlaq qiymatda har qanday oldindan belgilangan ijobiy sondan kamroq bo'ladi.

Agar sonlar ketma-ketligi haqiqiy son shaklida chegaraga ega bo'lsa, u chaqiriladi konvergent bu raqamga. Aks holda, ketma-ketlik chaqiriladi turlicha . Bundan tashqari, u cheksiz bo'lsa, uning chegarasi cheksizlikka teng deb hisoblanadi.

Bundan tashqari, agar chegaralanmagan ketma-ketlikning barcha elementlari ma'lum sondan boshlab musbat belgiga ega bo'lsa, unda bunday ketma-ketlikning chegarasi deyiladi. ortiqcha cheksizlik .

Agar chegaralanmagan ketma-ketlikning elementlari ma'lum sondan boshlab manfiy belgiga ega bo'lsa, ular bunday ketma-ketlikning chegarasi teng deb aytadilar. minus cheksizlik .

Ushbu ta'rifning halokatli kamchiligi bor: u chegara nima ekanligini tushuntiradi, lekin uni hisoblash usuli yoki uning mavjudligi haqida ma'lumot bermaydi. Bularning barchasi quyida isbotlangan limitning xususiyatlaridan kelib chiqadi.

Raqamlar ketma-ketligi.
Qanaqasiga ?

Ushbu darsda biz Vkontakte deb nomlangan katta hamjamiyat a'zolarining hayotidan juda ko'p qiziqarli narsalarni bilib olamiz raqamlar ketma-ketligi. Ko'rib chiqilayotgan mavzu nafaqat matematik tahlil kursiga, balki asoslarga ham tegishli. diskret matematika. Bundan tashqari, material minoraning boshqa qismlarini, xususan, o'rganish davomida o'zlashtirish uchun kerak bo'ladi raqamlar seriyasi Va funktsional qator. Siz buni juda muhim deb aytishingiz mumkin, rag'batlantiruvchi tarzda aytishingiz mumkin, bu oddiy, siz yana ko'plab muntazam iboralarni aytishingiz mumkin, lekin bugun maktabning birinchi, g'ayrioddiy dangasa haftasi, shuning uchun birinchi xatboshini yozish meni juda xafa qildi =) Men Men allaqachon faylni yuragimga saqlab qo'ygan edim va uxlashga tayyor bo'ldim, to'satdan ... boshimni samimiy e'tirof g'oyasi yoritib yubordi, bu mening qalbimni hayratlanarli darajada engillashtirdi va meni klaviaturada barmoqlarimni bosishni davom ettirishga undadi. .

Keling, yozgi xotiralardan tanaffus olib, bu hayajonli va ijobiy yangi dunyoga qaraylik ijtimoiy tarmoq:

Raqamlar ketma-ketligi haqida tushuncha

Birinchidan, so'zning o'zi haqida o'ylab ko'raylik: ketma-ketlik nima? Ketma-ketlik - biror narsadan keyin nimadir ketayotganda. Masalan, harakatlar ketma-ketligi, fasllar ketma-ketligi. Yoki kimdir kimdir orqasida joylashganida. Masalan, navbatdagi odamlarning ketma-ketligi, sug'orish teshigiga boradigan yo'lda fillar ketma-ketligi.

Keling, darhol aniqlik kiritamiz xarakterli xususiyatlar ketma-ketliklar. Birinchidan, ketma-ketlik a'zolari joylashgan qat'iy ravishda ma'lum bir tartibda. Shunday qilib, agar navbatdagi ikki kishi almashtirilsa, bu allaqachon bo'ladi boshqa keyingi ketma-ketlik. Ikkinchidan, hamma ketma-ketlik a'zosi Siz seriya raqamini belgilashingiz mumkin:

Raqamlar bilan ham xuddi shunday. Mayli hammaga tabiiy qiymat ba'zi qoidaga ko'ra mos haqiqiy raqam. Keyin ular sonli ketma-ketlik berilganligini aytishadi.

Ha, matematik masalalarda, farqli o'laroq hayotiy vaziyatlar ketma-ketlik deyarli har doim o'z ichiga oladi cheksiz ko'p raqamlar.

Ushbu holatda:
chaqirdi birinchi a'zo ketma-ketliklar;
– ikkinchi a'zo ketma-ketliklar;
– uchinchi a'zo ketma-ketliklar;
…
– nth yoki umumiy a'zo ketma-ketliklar;
…

Amalda, odatda, ketma-ketlik beriladi umumiy atama formulasi, Masalan:
- ijobiy juft sonlar ketma-ketligi:

Shunday qilib, yozuv ketma-ketlikning barcha a'zolarini noyob tarzda aniqlaydi - bu tabiiy qiymatlarga ko'ra qoida (formula). raqamlari yozishmalarga kiritiladi. Shuning uchun ketma-ketlik ko'pincha umumiy atama bilan qisqacha belgilanadi va "x" o'rniga boshqa lotin harflaridan foydalanish mumkin, masalan:

Ijobiy ketma-ketlik toq raqamlar :

Boshqa umumiy ketma-ketlik:

Ko'pchilik payqaganidek, "en" o'zgaruvchisi o'ziga xos hisoblagich rolini o'ynaydi.

Aslida, biz o'rta maktabda raqamlar ketma-ketligi bilan shug'ullanganmiz. Keling, eslaylik arifmetik progressiya. Men ta'rifni qayta yozmayman, keling, aniq bir misol bilan mohiyatga to'xtalib o'tamiz. Birinchi atama bo'lsin va - qadam arifmetik progressiya. Keyin:
– bu progressiyaning ikkinchi muddati;
– ushbu progressiyaning uchinchi muddati;
- to'rtinchi;
- beshinchi;
…
Va, shubhasiz, n-son berilgan takrorlanuvchi formula

Eslatma : takrorlanuvchi formulada har bir keyingi atama oldingi atama yoki hatto oldingi shartlarning butun majmuasi bilan ifodalanadi.

Olingan formuladan amalda unchalik foydasi yo'q - olish uchun, aytaylik, -ga, oldingi barcha shartlarni ko'rib chiqish kerak. Matematikada esa arifmetik progressiyaning n-chi hadi uchun qulayroq ifoda olingan: . Bizning holatda:

Formulaga natural sonlarni qo'ying va yuqorida tuzilgan sonlar ketma-ketligining to'g'riligini tekshiring.

Xuddi shunday hisob-kitoblar uchun ham amalga oshirilishi mumkin geometrik progressiya, n-chi hadi formula bilan berilgan, bu yerda birinchi had va – maxraj taraqqiyot. Matematik topshiriqlarda birinchi atama ko'pincha bittaga teng bo'ladi.

progressiya ketma-ketlikni belgilaydi ;
taraqqiyot ketma-ketlikni belgilaydi;
taraqqiyot ketma-ketlikni belgilaydi ;
taraqqiyot ketma-ketlikni belgilaydi .

Umid qilamanki, -1 toq kuchga -1 ga, juft kuchga esa birga teng ekanligini hamma biladi.

Progressiya deyiladi cheksiz kamayadi, agar (oxirgi ikki holat).

Keling, ikkita yangi do'stimizni ro'yxatimizga qo'shamiz, ulardan biri hozirgina monitor matritsasini taqillatgan:

Matematik jargondagi ketma-ketlik "miltillovchi" deb ataladi:

Shunday qilib, ketma-ketlik a'zolari takrorlanishi mumkin. Shunday qilib, ko'rib chiqilgan misolda ketma-ketlik ikkita cheksiz o'zgaruvchan sondan iborat.

Ketma-ket bir xil raqamlardan iborat bo'ladimi? Albatta. Misol uchun, u cheksiz sonli "uch" ni o'rnatadi. Estetiklar uchun formulada "en" hali ham rasmiy ravishda paydo bo'ladigan holat mavjud:

Keling, oddiy do'stimizni raqsga taklif qilaylik:

"en" cheksizlikka ko'tarilganda nima bo'ladi? Shubhasiz, ketma-ketlik a'zolari bo'ladi cheksiz yaqin nolga yaqinlashadi. Bu ketma-ketlikning chegarasi bo'lib, u quyidagicha yoziladi:

Agar ketma-ketlikning chegarasi nolga teng bo'lsa, u chaqiriladi cheksiz kichik.

Matematik analiz nazariyasida u berilgan ketma-ketlik chegarasining qat'iy ta'rifi epsilon mahallasi orqali. Keyingi maqola ushbu ta'rifga bag'ishlanadi, ammo hozircha uning ma'nosini ko'rib chiqamiz:

Raqam chizig'ida ketma-ketlik shartlarini va nolga (chegara) nisbatan qo'shni simmetriklikni tasvirlaymiz:


Endi ko'k joyni kaftlaringizning chetlari bilan chimchilab oling va uni chegaraga (qizil nuqta) tortib, kamaytirishni boshlang. Raqam - bu ketma-ketlikning chegarasi bo'lsa, FOR ANY oldindan tanlangan -mahalla (siz xohlagancha kichik) uning ichida bo'ladi cheksiz ko'p ketma-ketlik a'zolari va undan tashqarida - faqat final a'zolar soni (yoki umuman yo'q). Ya'ni, epsilon mahallasi mikroskopik va hatto kichikroq bo'lishi mumkin, ammo ketma-ketlikning "cheksiz dumi" ertami-kechmi bo'lishi kerak. to'liq hududga kiring.

Ketma-ketlik ham cheksizdir: farqi shundaki, uning a'zolari oldinga va orqaga sakrab o'tmaydi, lekin chegaraga faqat o'ngdan yaqinlashadi.

Tabiiyki, chegara har qanday boshqa chekli songa teng bo'lishi mumkin, elementar misol:

Bu erda kasr nolga intiladi va shunga mos ravishda chegara "ikki" ga teng.

Agar ketma-ketlik chekli chegara mavjud, keyin chaqiriladi konvergent(ayniqsa, cheksiz kichik da). Aks holda - turlicha, bu holda ikkita variant mumkin: yoki chegara umuman mavjud emas yoki cheksiz. Ikkinchi holda, ketma-ketlik chaqiriladi cheksiz katta. Keling, birinchi xatboshi misollarini ko'rib chiqaylik:

Ketma-ketliklar bor cheksiz katta, ularning a'zolari ishonch bilan "ortiqcha cheksizlik" sari harakat qilganda:

Birinchi had va qadamli arifmetik progressiya ham cheksiz katta:

Aytgancha, har qanday arifmetik progressiya ham farqlanadi, nol qadamli hol bundan mustasno - qachon . Bunday ketma-ketlikning chegarasi mavjud va birinchi muddatga to'g'ri keladi.

Ketma-ketliklar xuddi shunday taqdirga ega:

Har qanday cheksiz kamayib boruvchi geometrik progressiya, nomidan ko'rinib turibdiki, cheksiz kichik:

Agar geometrik progressiyaning maxraji bo'lsa, ketma-ketlik cheksiz katta bo'ladi:

Agar, masalan, chegara umuman mavjud bo'lmasa, chunki a'zolar tinmay yo "plyus cheksizlik" ga yoki "minus cheksizlik" ga o'tishadi. Va sog'lom fikr va Matan teoremalari shuni ko'rsatadiki, agar biror narsa biror joyga intilayotgan bo'lsa, bu yagona qadrli joy.

Bir oz vahiydan keyin Aytgancha, o'z-o'zidan ajralib turadigan nazoratsiz otish uchun "miltillovchi chiroq" aybdor ekanligi ayon bo'ladi.
Darhaqiqat, ketma-ketlik uchun, aytaylik, faqat –1 raqamini siqib chiqaradigan mahallani tanlash oson. Natijada cheksiz sonli ketma-ketlik a'zolari ("ortiqcha") bu mahalladan tashqarida qoladi. Ammo ta'rifga ko'ra, ma'lum bir momentdan (tabiiy son) ketma-ketlikning "cheksiz dumi" bo'lishi kerak to'liq chegarangizning istalgan yaqiniga kiring. Xulosa: osmon chegaradir.

Faktorial cheksiz katta ketma-ketlik:

Bundan tashqari, u sakrash va chegaralar bilan o'sib bormoqda, shuning uchun bu 100 dan ortiq raqamga (raqamlarga) ega bo'lgan raqam! Nega aynan 70? Unda mening muhandislik mikrokalkulyatorim rahm-shafqat so'raydi.

Tekshirish zarbasi bilan hamma narsa biroz murakkabroq va biz ma'ruzaning amaliy qismiga keldik, unda biz jangovar misollarni tahlil qilamiz:

Ammo endi siz kamida ikkita asosiy dars darajasida funktsiyalar chegaralarini hal qilishingiz kerak: Cheklovlar. Yechimlarga misollar Va Ajoyib chegaralar. Chunki ko'plab yechim usullari o'xshash bo'ladi. Ammo, birinchi navbatda, ketma-ketlik chegarasi va funktsiya chegarasi o'rtasidagi asosiy farqlarni tahlil qilaylik:

Ketma-ketlik chegarasida "dinamik" o'zgaruvchi "en" moyil bo'lishi mumkin faqat "ortiqcha cheksizlik" uchun- natural sonlarni oshirishga .
Funktsiya chegarasida "x" har qanday joyga - "ortiqcha / minus cheksizlik" ga yoki ixtiyoriy haqiqiy songa yo'naltirilishi mumkin.

Keyingi ketma-ketlik diskret(uzluksiz), ya'ni alohida ajratilgan a'zolardan iborat. Bir, ikki, uch, to'rt, besh, quyon sayrga chiqdi. Funksiya argumenti uzluksizligi bilan tavsiflanadi, ya'ni "X" muammosiz, u yoki bu qiymatga intiladi. Va shunga ko'ra, funktsiya qiymatlari ham doimiy ravishda o'z chegarasiga yaqinlashadi.

Sababi uchun diskretlik ketma-ketliklar ichida faktoriallar, "miltillovchi chiroqlar", progressiyalar va boshqalar kabi o'ziga xos belgilar mavjud. Va endi men ketma-ketliklarga xos bo'lgan chegaralarni tahlil qilishga harakat qilaman.

Progressiyadan boshlaylik:

1-misol

Ketma-ketlik chegarasini toping

Yechim: cheksiz kamayuvchi geometrik progressiyaga o'xshash narsa, lekin bu haqiqatan ham shundaymi? Aniqlik uchun keling, dastlabki bir nechta atamalarni yozamiz:

O'shandan beri biz gaplashamiz miqdori formula bilan hisoblangan cheksiz kamayuvchi geometrik progressiyaning hadlari.

Keling, qaror qabul qilaylik:

Cheksiz kamayuvchi geometrik progressiya yig'indisi formulasidan foydalanamiz: . Bunda: – birinchi had, – progressiyaning maxraji.

2-misol

Ketma-ketlikning dastlabki to‘rtta hadini yozing va uning chegarasini toping

Bu siz o'zingiz hal qilishingiz uchun misoldir. Numeratordagi noaniqlikni bartaraf qilish uchun arifmetik progressiyaning birinchi hadlari yig'indisi formulasini qo'llash kerak bo'ladi:
, bu yerda birinchi va a progressiyaning n-chi hadi.

Ketma-ketliklar ichida "en" har doim "ortiqcha cheksizlik" ga moyil bo'lganligi sababli, noaniqlik eng mashhurlaridan biri bo'lishi ajablanarli emas.
Va ko'pgina misollar funksiya chegaralari bilan bir xil tarzda hal qilinadi!

Yoki, ehtimol, shunga o'xshash murakkabroq narsa ? Maqolaning 3-misolini ko'rib chiqing Limitlarni yechish usullari.

Rasmiy nuqtai nazardan, farq faqat bitta harfda bo'ladi - bu erda "x" va bu erda "en".
Texnika bir xil - hisoblagich va maxraj eng yuqori darajada "en" ga bo'linishi kerak.

Bundan tashqari, ketma-ketliklar ichida noaniqlik juda keng tarqalgan. Xuddi shu maqolaning 11-13-misollaridan chegaralarni qanday hal qilishni o'rganishingiz mumkin.

Cheklovni tushunish uchun darsning 7-misoliga qarang Ajoyib chegaralar(ikkinchi ajoyib chegara diskret holat uchun ham amal qiladi). Yechim yana bitta harf farqi bilan uglerod nusxasi kabi bo'ladi.

Keyingi to‘rtta misol (3-6-raqamlar) ham “ikki yuzli”dir, lekin amalda negadir ular funksiya chegaralaridan ko‘ra ketma-ketlik chegaralariga ko‘proq xosdir:

3-misol

Ketma-ketlik chegarasini toping

Yechim: avval to'liq yechim, keyin bosqichma-bosqich sharhlar:

(1) Numeratorda biz formuladan ikki marta foydalanamiz.

(2) Biz taqdim etamiz o'xshash atamalar hisoblagichda.

(3) Noaniqlikni bartaraf qilish uchun pay va maxrajni ("en" ga eng yuqori darajaga) bo'ling.

Ko'rib turganingizdek, hech qanday murakkab narsa yo'q.

4-misol

Ketma-ketlik chegarasini toping

Bu siz o'zingiz hal qilishingiz uchun misol, qisqartirilgan ko'paytirish formulalari yordam berish.

s ichida indikativ Ketma-ketliklarda pay va maxrajni bo'lishning o'xshash usuli qo'llaniladi:

5-misol

Ketma-ketlik chegarasini toping

Yechim Keling, uni xuddi shu sxema bo'yicha tartibga keltiramiz:

Aytgancha, xuddi shunday teorema funktsiyalar uchun ham to'g'ri: cheksiz bilan cheklangan funktsiyaning mahsuloti. kichik funktsiya- cheksiz kichik funksiyadir.

9-misol

Ketma-ketlik chegarasini toping

Chegaraga ega bo'lgan sonli ketma-ketliklarning asosiy teoremalari va xossalarining formulalari berilgan. Ketma-ketlik ta'rifi va uning chegarasini o'z ichiga oladi. Ketma-ketliklar bilan arifmetik amallar, tengsizliklar bilan bog'liq xossalar, yaqinlashish mezonlari, cheksiz kichik va cheksiz katta ketma-ketliklarning xossalari ko'rib chiqiladi.

Tarkib

Ketma-ketliklarning chekli chegaralarining xossalari

Asosiy xususiyatlar

A nuqta ketma-ketlikning chegarasi, agar bu nuqtaning biron bir qo'shnisidan tashqarida bo'lsa elementlarning chekli soni ketma-ketliklar yoki bo'sh to'plam.

Agar a soni ketma-ketlikning chegarasi bo'lmasa, u holda a nuqtaning qo'shnisi mavjud bo'lib, undan keyin ham mavjud. ketma-ketlik elementlarining cheksiz soni.

Sonlar ketma-ketligi chegarasi uchun yagonalik teoremasi. Agar ketma-ketlik chegarasiga ega bo'lsa, u noyobdir.

Agar ketma-ketlikning chekli chegarasi bo'lsa, u holda cheklangan.

Agar ketma-ketlikning har bir elementi bir xil raqamga teng C: u holda bu ketma-ketlikning chegarasi bor, soniga teng C.

Agar ketma-ketlik birinchi m elementni qo'shish, o'chirish yoki o'zgartirish, keyin bu uning yaqinlashuviga ta'sir qilmaydi.

Asosiy xususiyatlarning dalillari sahifasida berilgan
Ketma-ketliklarning chekli chegaralarining asosiy xossalari >>>.

Limitli arifmetik amallar

Ikkala ketma-ketlikning ham chekli chegaralari bo'lsin. Va C doimiy bo'lsin, ya'ni berilgan raqam
;
;
;
. Keyin
, Agar .

Ko'rsatkich bo'lsa, barcha n uchun, deb faraz qilinadi.

Agar, keyin. Isbot sahifasida berilgan
arifmetik xususiyatlar

Ketma-ketliklarning chekli chegaralarining arifmetik xossalari >>>.

Tengsizliklar bilan bog'liq xususiyatlar

Agar ma'lum sondan boshlab ketma-ketlik elementlari tengsizlikni qanoatlantirsa, u holda bu ketma-ketlikning chegarasi a tengsizlikni ham qanoatlantiradi.

Agar ma'lum sondan boshlab ketma-ketlik elementlari yopiq intervalga (segmentga) tegishli bo'lsa, a chegarasi ham shu intervalga tegishli: .

Agar ma'lum sondan boshlab ketma-ketliklarning va va elementlari tengsizlikni qanoatlantirsa, u holda .
Agar va, qandaydir sondan boshlab, , bo'lsa.
Xususan, agar, qandaydir sondan boshlab, , keyin
bo'lsa, keyin;

bo'lsa, keyin.

Agar va bo'lsa, unda. < b Tinch qo'y, hamma narsa o'z holidagiday qo'sin; shunday bo'lsin. Agar a , u holda barcha n uchun N natural son mavjud> N

tengsizlik mavjud. sahifasida berilgan
Tengsizliklar bilan bog'liq xususiyatlarni isbotlash

Tengsizliklar bilan bog'liq ketma-ketlik chegaralarining xossalari >>>.

Cheksiz katta va cheksiz kichik ketma-ketliklar

Cheksiz kichik ketma-ketlik
.

Cheksiz kichik ketma-ketlik chegarasi nolga teng bo'lgan ketma-ketlikdir: Yig'indi va farq

chekli sonli cheksiz kichik ketma-ketlikning cheksiz kichik ketma-ketligidir. Cheklangan ketma-ketlikning mahsuloti

to infinitesima - cheksiz kichik ketma-ketlik. Cheklangan sonning mahsuloti

Ketma-ketlik a chegarasiga ega bo'lishi uchun bu zarur va etarli bo'ladi, bu erda cheksiz kichik ketma-ketlik.

Cheksiz kichik ketma-ketliklarning xossalarini isbotlash sahifasida berilgan
Infinitesimal ketma-ketliklar - ta'rifi va xossalari >>>.

Cheksiz katta ketma-ketlik

Cheksiz katta ketma-ketlik cheksiz katta chegaraga ega bo'lgan ketma-ketlikdir. Ya'ni, agar har qanday musbat son uchun N natural son mavjud bo'lsa, barcha natural sonlar uchun tengsizlik amal qiladi.
.
Bunday holda, ular yozadilar
.
Yoki da.
Ularning aytishicha, bu cheksizlikka intiladi.

Agar ba'zi bir N raqamidan boshlab, u holda
.
Agar unda
.

Agar ketma-ketlik cheksiz katta bo'lsa, u holda N sonidan boshlab cheksiz kichik bo'lgan ketma-ketlik aniqlanadi. Agar nolga teng bo'lmagan elementlarga ega bo'lgan cheksiz kichik ketma-ketlik bo'lsa, unda ketma-ketlik cheksiz katta.

Agar ketma-ketlik cheksiz katta bo'lsa va ketma-ketlik cheklangan bo'lsa, u holda
.

Agar ketma-ketlik elementlarining mutlaq qiymatlari pastdan musbat son () bilan cheklangan bo'lsa va nolga teng bo'lmagan elementlar bilan cheksiz kichik bo'lsa, u holda
.

Batafsil ma'lumot misollar bilan cheksiz katta ketma-ketlikning ta'rifi sahifasida berilgan
Cheksiz katta ketma-ketlikning ta'rifi >>>.
Cheksiz katta ketma-ketliklarning xossalarini isbotlash sahifasida berilgan
Cheksiz katta ketma-ketliklarning xossalari >>> .

Ketma-ket yaqinlashish mezonlari

Monoton ketma-ketliklar

Qat'iy ortib boruvchi ketma-ketlik barcha elementlari quyidagi tengsizliklarni qondiradigan ketma-ketlikdir:
.

Shu kabi tengsizliklar boshqa monotonik ketma-ketliklarni belgilaydi.

Qat'iy kamayib boruvchi ketma-ketlik:
.
Kamaymaydigan ketma-ketlik:
.
O'smaydigan ketma-ketlik:
.

Bundan kelib chiqadiki, qat'iy ortib boruvchi ketma-ketlik ham kamaymaydi. Qattiq kamayib boruvchi ketma-ketlik ham ortib bormaydi.

Monotonik ketma-ketlik kamaymaydigan yoki ortib bormaydigan ketma-ketlikdir.

Monotonik ketma-ketlik kamida bir tomondan qiymat bilan cheklangan.

Kamaymaydigan ketma-ketlik quyida chegaralangan: . O'smaydigan ketma-ketlik yuqoridan chegaralangan: .

Har qanday kamaymaydigan (o'smaydigan) ketma-ketlik pastdan (yuqoridan) chegaralanganligi sababli, Veyershtrass teoremasini quyidagicha ifodalash mumkin:

Monotonik ketma-ketlikning chekli chegarasi bo'lishi uchun uning chegaralangan bo'lishi zarur va etarli: .

Monotonik chegaralanmagan ketma-ketlik kamaymaydigan va o'smaydigan ketma-ketlik uchun teng cheksiz chegaraga ega.

Veyershtras teoremasining isboti sahifada berilgan
Monoton ketma-ketlikning chegarasi haqidagi Veyershtras teoremasi >>>.

Ketma-ket yaqinlashish uchun Koshi mezoni

Koshi holati
Muvofiqlik qanoatlantiradi Koshi holati, agar birortasi uchun natural son mavjud bo'lsa, hamma uchun natural sonlar n va m shartni qanoatlantirsa, tengsizlik qanoatlantiriladi
.

Asosiy ketma-ketlik qanoatlantiradigan ketma-ketlikdir Koshi holati.

Ketma-ket yaqinlashish uchun Koshi mezoni. Ketma-ketlik chekli chegaraga ega bo'lishi uchun uning Koshi shartini qondirishi zarur va yetarlidir.

Koshining yaqinlashish mezonining isboti sahifada berilgan
Ketma-ketlikning yaqinlashuvining Koshi mezoni >>>.

Quyi ketma-ketliklar

Bolzano-Vayershtrass teoremasi. Har qanday chegaralangan ketma-ketlikdan konvergent quyi ketma-ketlikni tanlash mumkin. Va har qanday chegaralanmagan ketma-ketlikdan - ga yoki ga yaqinlashuvchi cheksiz katta kichik ketma-ketlik.

Bolzano-Veyershtras teoremasining isboti sahifada berilgan
Bolzano-Vayershtras teoremasi >>> .

Sahifada pastki ketma-ketliklar va qisman chegaralarning ta'riflari, teoremalari va xususiyatlari muhokama qilinadi
Ketma-ketliklarning pastki ketma-ketliklari va qisman chegaralari >>>.

Foydalanilgan adabiyotlar:
CM. Nikolskiy. Matematik tahlil kursi. 1-jild. Moskva, 1983 yil.
L.D. Kudryavtsev. Matematik tahlil kursi. 1-jild. Moskva, 2003 yil.
V.A. Zorich. Matematik tahlil. 1-qism. Moskva, 1997 yil.
V.A. Ilyin, E.G. Poznyak. Matematik analiz asoslari. 1-qism. Moskva, 2005 yil.

Shuningdek qarang: