Garmonik chiziqlilashtirish usuli: Laboratoriya ishi uchun ko'rsatmalar. Garmonik chiziqlilanish Garmonik chiziqlilanish koeffitsientlari

14.08.2021

Rossiya Federatsiyasi Ta'lim va fan vazirligi

Saratov davlat texnika universiteti

Balakovo muhandislik, texnologiya va menejment instituti

Garmonik linearizatsiya usuli

Ko'rsatmalar 210100 ixtisosligi talabalari uchun "Avtomatik boshqaruv nazariyasi" kursi bo'yicha laboratoriya ishlari uchun

Tasdiqlangan

tahririyat va nashriyot kengashi

Balakovo texnologiya instituti,

texnologiya va boshqaruv

Balakovo 2004 yil

Ishning maqsadi: Garmonik linearizatsiya (garmonik muvozanat) usuli yordamida chiziqli bo'lmagan tizimlarni o'rganish, turli nochiziqli bog'lanishlar uchun garmonik chiziqlilanish koeffitsientlarini aniqlash. Doimiy amplitudali va chastotali simmetrik tebranishlar parametrlarini (o‘z-o‘zidan tebranishlar) topish, algebraik, chastotali usullar yordamida, shuningdek Mixaylov mezonidan foydalanish ko‘nikmalarini egallash.

ASOSIY MA'LUMOT

Garmonik linearizatsiya usuli chiziqli bo'lmagan tizimlarni o'rganishning taxminiy usullarini anglatadi. Bu juda sodda va maqbul aniqlik bilan chiziqli bo'lmagan tizimlarning barqarorligini baholash va tizimda o'rnatilgan tebranishlarning chastotasi va amplitudasini aniqlash imkonini beradi.

O'rganilayotgan chiziqli bo'lmagan ACS quyidagi shaklda ifodalanishi mumkin deb taxmin qilinadi

va chiziqli bo'lmagan qism bitta chiziqli bo'lmagan bo'lishi kerak

. (1)

Bu chiziqli bo'lmaganlik uzluksiz yoki o'rni, bir qiymatli yoki histeretik bo'lishi mumkin.

Har qanday funktsiya yoki signal chiziqli mustaqil, ma'lum bir holatda ortonormal funktsiyalar tizimiga muvofiq qatorga kengaytirilishi mumkin. Bunday ortogonal qator sifatida Furye qatoridan foydalanish mumkin.

Tizimning chiziqli bo'lmagan qismining chiqish signalini Furye qatoriga kengaytiramiz

, (2)

bu erda Furye koeffitsientlari,

. (3)

Shunday qilib, (2) ga muvofiq signal chastotalar ortib borayotgan harmonikalarning cheksiz yig'indisi sifatida ifodalanishi mumkin. va hokazo. Ushbu signal chiziqli bo'lmagan tizimning chiziqli qismining kirishiga beriladi.

Chiziqli qismning uzatish funksiyasini belgilaymiz

, (4)

va sanoqli ko'phadning darajasi maxraj ko'phadning darajasidan kichik bo'lishi kerak. Bunday holda, chiziqli qismning chastotali javobi shaklga ega

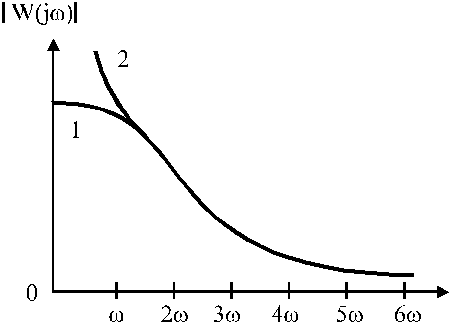
bu erda 1 - qutblari yo'q, 2 - qutb yoki qutbga ega.

Chastota javobi uchun yozish adolatli

Shunday qilib, chiziqli bo'lmagan tizimning chiziqli qismi yuqori o'tkazuvchan filtrdir. Bunday holda, chiziqli qism faqat past chastotalarni zaiflashtirmasdan uzatadi, yuqori chastotalar esa chastota ortishi bilan sezilarli darajada zaiflashadi.

Garmonik chiziqlilashtirish usulida tizimning chiziqli qismi faqat signalning doimiy to'g'ridan-to'g'ri komponenti va birinchi garmonikadan o'tadi, deb taxmin qilinadi. Keyin chiziqli qismning chiqishidagi signal shaklga ega bo'ladi

Bu signal tizimning butun yopiq sxemasidan 1-rasm va chiziqli bo'lmagan elementning chiqishida yuqori harmoniklarni hisobga olmasdan o'tadi, (2) ga binoan biz

. (7)

Chiziqli bo'lmagan tizimlarni garmonik linearizatsiya usulidan foydalangan holda o'rganishda nosimmetrik va assimetrik tebranish holatlari mumkin. Simmetrik tebranishlar holatini ko'rib chiqamiz. Bu erda va.

Keling, quyidagi belgini kiritamiz

Ularni (7) ga almashtirsak, biz . (8)

Shuni hisobga olib

, qayerda ,

. (9)

(3) va (8) ga binoan qachon

. (10)

Ifoda (9) - chiziqli bo'lmaganlikning garmonik linearizatsiyasi da kirish o'zgaruvchisi va chiqish o'zgaruvchisi o'rtasida chiziqli munosabatni o'rnatadi. Miqdorlar garmonik linearizatsiya koeffitsientlari deb ataladi.

Shuni ta'kidlash kerakki, (9) tenglama aniq miqdorlar va (tizimdagi garmonik tebranishlarning amplitudasi va chastotasi) uchun chiziqli. Ammo umuman olganda, u chiziqli bo'lmagan xususiyatlarni saqlaydi, chunki koeffitsientlar har xil va uchun har xil. Bu xususiyat nochiziqli tizimlarning xossalarini garmonik linearizatsiya usuli yordamida o'rganish imkonini beradi [Popov E.P.].

Asimmetrik tebranishlar bo'lsa, chiziqli bo'lmaganlikning garmonik linearizatsiyasi chiziqli tenglamaga olib keladi.

. (12)

Xuddi (9) tenglama singari, chiziqli tenglama (11) chiziqli bo'lmagan elementning xususiyatlarini saqlab qoladi, chunki garmonik chiziqlilanish koeffitsientlari , , shuningdek, doimiy komponent ham garmonik tebranishlarning siljishi va amplitudasiga bog'liq.

(9) va (11) tenglamalar garmonik chiziqli chiziqli bo'lmagan elementlarning uzatish funksiyalarini olish imkonini beradi. Shunday qilib, nosimmetrik tebranishlar uchun

Ushbu bobda har qanday tartibli chiziqli bo'lmagan tizimlarning davriy yechimlarini (o'z-o'zidan tebranishlarini) va barqarorligini taxminiy aniqlash uchun garmonik linearizatsiya usuli ko'rsatilgan, bu g'oyaga ko'ra ekvivalent chiziqlilashtirish usuliga yoki N. M. Krilovning garmonik muvozanat usuliga yaqin. N. N. Bogolyubov va natijalarga ko'ra - B.V.Bulgakovning kichik parametr usuliga ham.

Ko'rib chiqilayotgan taxminiy usul chiziqli bo'lmagan avtomatik tizimlarni o'rganish uchun kuchli vosita bo'lib, uning apparatlarining soddaligi va juda ko'p qirraliligi nuqtai nazaridan juda ko'p chiziqli bo'lmagan holatlarga nisbatan qo'llaniladi. Biroq, bu muammoni taxminan hal qilishini yodda tutish kerak. Uni qo'llashda ma'lum cheklovlar mavjud, ular quyida muhokama qilinadi. Bu cheklovlar odatda avtomatik boshqaruv nazariyasi muammolarida yaxshi kuzatiladi. Amaliy hisob-kitoblar va eksperimentlar chiziqli bo'lmagan tizimlarning ko'p turlari uchun ushbu usulning maqbulligini ko'rsatadi.

Shaklning qandaydir chiziqli bo'lmagan ifodasi berilsin

Ifodaning o'ng tomonidagi funktsiyani (18.1) Furye qatoriga kengaytirib, olamiz

bu kengayishda doimiy komponentning yo'qligini anglatadi. Ushbu bobda doimiy komponentning yo'qligi sharti (18.5) qondiriladi deb taxmin qilinadi. Keyinchalik (19-bob) o'z-o'zidan tebranishlarni doimiy komponent mavjudligida, ya'ni shart bajarilmaganda (18.5) o'rganish usuli beriladi.

Agar (18.2) va (18.3) dan shuni hisobga olsak.

u holda (18.5) shartdagi formula (18.4) shaklda yozilishi mumkin

Bu erda q - formulalar bilan aniqlanadigan garmonik chiziqli koeffitsientlar:

Shunday qilib, chiziqli bo'lmagan ifoda (18.1) yuqori harmonikalargacha chiziqliga o'xshash (18.6) ifoda bilan almashtiriladi. Bu operatsiya garmonik linearizatsiya deb ataladi. Koeffitsientlar doimiy qiymatlarda, ya'ni davriy jarayonda doimiydir. Vaqtinchalik tebranish jarayonida a va co ning o'zgarishi bilan q va koeffitsientlari o'zgaradi (20-bobga qarang). Davriy jarayonlarning turli amplitudalari va chastotalari uchun ifoda koeffitsientlari (18.6) kattalik jihatidan har xil bo'ladi. Keyinchalik muhokama qilish uchun juda muhim bo'lgan bu holat odatiy chiziqlilashtirish usuli (§ 3.1) bilan solishtirganda garmonik linearizatsiya o'rtasidagi sezilarli farq bo'lib, kitobning oldingi bo'limlarida ishlatilgan sof chiziqli ifodalarga olib keladi. Bu holat chiziqli tadqiqot usullarini ifodalashda (18.6) qo'llash orqali nochiziqli tizimlarning an'anaviy linearizatsiya bilan aniqlanmaydigan asosiy xususiyatlarini tahlil qilish imkonini beradi.

Biz, shuningdek, oddiy chiziqli bo'lmaganlik uchun garmonik linearizatsiya formulalarini taqdim etamiz:

Bu erda ikkita variant mavjud: 1) egri chiziqda histerezis halqasi mavjud (masalan, 16.18-rasm, c, 16.22-rasm, d, e) va 2) egri chiziqda histerezis halqasi yo'q (16.8-rasm, b). , 16.22-rasm, a va boshqalar).

Gisterezis halqasi mavjud bo'lganda, hosilaning belgisiga bog'liqlik haqiqatda kuzatilganda, chiziqli bo'lmagan funksiya garmonik linearizatsiyadan keyin u quyidagi ifoda bilan almashtiriladi (bilan

doimiy komponent bo'lmasa:

Agar egri chiziqda histerezis halqasi bo'lmasa, u holda bo'ladi

(gisterezis halqasi bilan bu integral o'sish va pasayish paytida egri chiziq konturidagi farq tufayli nolga teng emas edi.

Shunday qilib, histerezis halqasi bo'lmasa, chiziqli bo'lmagan ifoda (18.8) oddiyroq bilan almashtiriladi:

ya'ni yuqori harmoniklarga to'g'ri keladigan egri chiziqli yoki singan xarakteristika to'g'ri chiziqli bilan almashtiriladi, uning qiyaligi q tebranish amplitudasining kattaligiga bog'liq. Boshqacha qilib aytadigan bo'lsak, chiziqli bo'lmagan bog'lanish x kirish miqdori tebranishlarining a amplitudasiga bog'liq bo'lgan tishli nisbati (qo'shimcha) bilan "chiziqli" bilan taqqoslanadi.

(18.9) ga ko'ra, histerezis halqasi, qo'shimcha ravishda, faza kechikishini beruvchi lotinni kiritadi, chunki Shunday qilib, histerezis halqasi ko'rinishidagi chiziqli bo'lmagan koordinatali kechikish garmonik linearizatsiya paytida ekvivalent chiziqli faza kechikishiga aylanadi.

Etakchi pastadir bilan maxsus nochiziqli bog'lanishni yaratish mumkin, bu lotinni kiritishda chiziqli faza avansiga teng bo'ladi, ammo farq bilan faza avansning kattaligi tebranish amplitudasining o'lchamiga bog'liq bo'ladi. chiziqli tizimlarda bunday emas.

Chiziqli bo'lmagan bog'lanish turli chiziqli va chiziqli bo'lmagan ifodalar yig'indisini o'z ichiga olgan murakkab tenglama bilan tavsiflangan hollarda, chiziqli bo'lmagan atamalarning har biri alohida garmonik linearizatsiyaga duchor bo'ladi. Nochiziqlilik mahsuloti majburiy ravishda bitta murakkab chiziqli bo'lmaganlik sifatida bir butun sifatida ko'rib chiqiladi. Bunday holda, boshqa tabiatdagi chiziqli bo'lmagan funktsiyalar paydo bo'lishi mumkin.

Masalan, (16.3) ikkinchi tenglamaning garmonik linearizatsiyasi bilan siz da funksiya bilan shug'ullanishingiz kerak bo'ladi. Bunday holda biz olamiz

sharti bilan; inobatga olgan holda

Agar funktsiya yoki funktsiya chiziqli bo'lmagan bog'lanish tenglamasida yagona chiziqli bo'lmagan funksiya bo'lsa, u holda harmonik bilan

linearizatsiya biz qo'yishimiz mumkin va

oldingi formulalarga o'xshash (18.6) va (18.7). Ammo bu holda, barcha hisob-kitoblarda a ning qiymati x koordinatasining o'zi emas, balki tezlik tebranishlarining amplitudasi bo'ladi. Keyin ikkinchisi amplitudaga ega bo'ladi

Formulalar (18.10) yordamida harmonik linearizatsiya koeffitsientlarini hisoblashda shuni yodda tutish kerakki, nosimmetrik nochiziqli xarakteristikalar uchun integralni ikki barobarga oshirish orqali olish mumkin, ya'ni.

va hisoblashda koordinatalarning kelib chiqishiga nisbatan simmetrik bo'lgan histerezsiz xarakteristikalar uchun yozish mumkin.

Keling, eng oddiy chiziqli bo'lmagan bog'lanishlarning koeffitsientlari uchun ifodalarni keltiramiz. Keyinchalik ular turli xil muammolarni hal qilish uchun bevosita ishlatilishi mumkin.

O'rni zvenolarini garmonik linearizatsiya koeffitsientlari. Formulalar yordamida (18.10) eng tipik o'rni bo'g'inlarining koeffitsientlari va tenglamalarini topamiz. Keling, rasmdagi grafikda tasvirlangan o'rni aloqasining xususiyatlarini umumiy ko'rib chiqaylik. 18.1, a, agar mavjud bo'lsa kasr son oraliqda

Maxsus holatlar sifatida boshqa turdagi o'rni aloqalarining tenglamalari olinadi.

Agar kirish miqdorining tebranishlari amplitudaga ega bo'lsa, u holda rasmga muvofiq. 18.1, lekin tizimda hech qanday harakat bo'lmaydi. Agar amplituda keyin o'rni kalitlari A, B, C, D nuqtalarida sodir bo'ladi (18.1-rasm, b), bizda mavjud

Shunday qilib, xususiyatlardan foydalangandan so'ng, (18.10) integrallarning har biri uchta atamaga bo'linadi:

va ularning birinchi va uchinchisi shaklga muvofiq. 18.1 va va nol bo'ladi. Shuning uchun (18.10) ifodalar shaklni oladi

va rasmga o'xshash xarakteristikaga ega o'rni aloqasi tenglamasi. 18.1, lekin bu erda olingan qiymatlar bilan (18.9) shaklga ega bo'ladi.

Keling, alohida holatlarni ko'rib chiqaylik.

Histerez halqasi bo'lmagan xarakteristikaga ega, lekin o'lik zonaga ega bo'lgan o'rni aloqasi uchun (18.1-rasm, a), yuqoridagi formulalardan faraz qilamiz.

Shakl kabi histerezis pastadirli o'rni xarakteristikasi uchun. bor deb faraz qilamiz

Nihoyat, ideal o'rni havolasi uchun (18.1-rasm, e), biz topamiz deb faraz qilamiz

Oxirgi misolda rele xarakteristikasining garmonik chiziqlilashuvining ma'nosini ko'rish oson. q ning yozma ifodasi siniq chiziqni to'g'ri chiziq bilan almashtirishni anglatadi (18.1-rasm, e) bu to'g'ri chiziq taxminan berilgan amplituda a bilan qoplangan siniq chiziq kesimini almashtiradi. Bu erdan hamma narsa aniq bo'ladi proportsional bog'liqlik(18.18) formula bo'yicha berilgan a dan, chunki kirish qiymatining tebranishlarining a amplitudasi qanchalik katta bo'lsa, to'g'ri chiziq shunchalik tekis bo'lishi kerak, taxminan singan chiziq o'rnini bosadi.

Vaziyat rasmdagi o'rni xarakteristikasi bilan o'xshash. 18.1, d buning uchun uning o'rnini bosuvchi to'g'ri chiziqning qiyaligi (18.16) formula bilan berilgan. Binobarin, tebranish jarayonidagi har qanday histerezsiz o'rni aloqasi shunday "chiziqli" bog'lanishga teng bo'lib, uning tishli nisbati (qo'shimchasi) kirish miqdori tebranishlari amplitudasining ortishi bilan kamayadi.

Gisterezis halqali o'rni bo'g'iniga kelsak, (18.9) va (18.17) ga binoan u avvalgisiga o'xshash daromadli chiziqli bog'lanish bilan almashtiriladi, ammo qo'shimcha ravishda o'ng tomonda salbiy lotin kiritiladi. tenglamaning tomoni. Ijobiydan farqli ravishda salbiy lotinning kiritilishi (10.2-bandga qarang) havolaning kirish harakatiga javobida fazali kechikishni keltirib chiqaradi. Bu histerezis halqasi ko'rinishidagi chiziqli bo'lmaganlik ta'sirini almashtiradigan "chiziqli ekvivalent" bo'lib xizmat qiladi. Xuddi o'sha payt

(18.17) ga muvofiq hosila koeffitsienti ham kirish miqdori tebranishlarining a amplitudasi ortishi bilan kamayadi, bu tushunarli, chunki histerezis halqasining o'rni aloqasidagi tebranishlar jarayoniga ta'siri kichikroq bo'lishi kerak, histerezis halqasining kengligi bilan solishtirganda tebranishlarning amplitudasi qanchalik katta bo'lsa.

Boshqa eng oddiy chiziqli bo'lmagan bog'lanishlarning garmonik linearizatsiya koeffitsientlari. Keling, o'lik zona va to'yinganlik bilan chiziqli bo'lmagan bog'lanishni ko'rib chiqaylik (18.2-rasm, a). Rasmga ko'ra. 18.2, b, qaerda

bo'limdagi integral (18.10) besh hadga bo'linadi va ulardan ikkitasi nolga teng. Shunung uchun

almashtirish bilan biz qayerdan olamiz

bu erda (18.19) formulalar bilan aniqlanadi. Bu erda histerezis halqasi yo'qligi sababli

Shunday qilib, rasmga o'xshash xarakteristikaga ega bo'lmagan chiziqli bog'lanish tenglamasi. 18.2 va bu erda (18.20) ifoda bilan aniqlanadi.

Maxsus holat sifatida, bu to'yinganliksiz o'lik zonaga ega bo'lgan havola uchun qiymatni beradi (18.2-rasm, s). Buning uchun oldingi yechimda biz qo'yishimiz kerak va shuning uchun, Keyin

Ko'rib turganimizdek, o'lik zonaga ega bo'lgan bog'lanish bu erda uning hisobidan daromad kamaygan chiziqli bog'lanishga o'xshatiladi. Daromadning bu kamayishi kichik amplitudalarda muhim va katta bo'lganlarda kichik va da

Kirish

Avtomatik boshqarish amaliyotida releli tizimlar keng tarqaldi. O'rni tizimlarining afzalligi - dizaynning soddaligi, ishonchliligi, texnik xizmat ko'rsatish va konfiguratsiyaning qulayligi. O'rni tizimlari chiziqli bo'lmagan avtomatik boshqaruv tizimlarining maxsus sinfini ifodalaydi.

O'rni tizimlarida uzluksiz bo'lganlardan farqli o'laroq, tartibga solish harakati o'rni boshqaruv signali (ko'pincha bu boshqaruv xatosi) ba'zi bir belgilangan (eshik) qiymatlardan, masalan, noldan o'tganda keskin o'zgaradi.

O'rni tizimlari, qoida tariqasida, yuqori ko'rsatkichlarga ega, chunki ulardagi boshqaruv harakati deyarli bir zumda o'zgaradi va aktuator maksimal amplitudaning bo'lak-bo'lak doimiy signaliga ta'sir qiladi. Shu bilan birga, o'z-o'zidan tebranishlar ko'pincha o'rni tizimlarida sodir bo'ladi, bu ko'p hollarda kamchilikdir. Ushbu maqolada to'rt xil boshqaruv qonuniga ega bo'lgan rele tizimi o'rganiladi.

O'rganilayotgan tizimning tuzilishi

O'rganilayotgan tizim (rasm) 1 taqqoslash elementi ES, o'rni elementi RE, aktuator (qo'shimchasi = 1 bo'lgan ideal integrator), boshqaruv ob'ektini (uch vaqt doimiysi , va daromadli aperiodik bog'lanish) o'z ichiga oladi. Tizim parametrlarining qiymatlari jadvalda keltirilgan. 1-ilova A.

O'rganilayotgan o'rni elementlarining statik xarakteristikalari (kirish-chiqish xarakteristikalari) rasmda ko'rsatilgan. 2.

Shaklda. 2a ideal ikki pozitsiyali o'rni xususiyatlarini ko'rsatadi, rasm. 2b o'lik zonali uch pozitsiyali o'rni xarakteristikasi. Shaklda. 2,c va 2,d mos ravishda musbat va manfiy histerezisli ikki pozitsiyali rele xarakteristikalarini ko'rsatadi.

Tekshirilayotgan ASR ni SIAM yoki VisSim kabi taniqli modellashtirish paketlari yordamida modellashtirish mumkin.

Izoh. Ba'zi simulyatsiya paketlarida chiqish qiymati

o'rni signali ±B o'rniga faqat ±1 qiymatlarni qabul qilishi mumkin, bu erda B ixtiyoriy sondir. Bunday hollarda integrator daromadini ga teng qabul qilish kerak.

Ish tartibi

Ishni bajarish uchun har bir talaba o'qituvchidan dastlabki ma'lumotlarning versiyasini oladi (2-bo'limga qarang).

Ish ikki bosqichda amalga oshiriladi.

Birinchi bosqich - hisoblash va tadqiqot (laboratoriyadan tashqarida amalga oshirilishi mumkin).

Ikkinchi bosqich eksperimental (laboratoriyada o'tkaziladi). Bu bosqichda paketlardan biri yordamida birinchi bosqichda hisoblangan rejimlar uchun o‘rganilayotgan tizimdagi o‘tkinchi jarayonlar simulyatsiya qilinadi va nazariy usullarning to‘g‘riligi tekshiriladi.

Kerakli nazariy material 4-bo'limda keltirilgan; 5-bo'limda test savollari mavjud.

3.1. Hisoblash va tadqiqot qismi

1. Tizimning chiziqli qismining amplituda-chastota va faza-chastota, haqiqiy va xayoliy xarakteristikalari uchun ifodalarni oling.

2. Tizimning chiziqli qismining amplituda-faza xarakteristikasini hisoblang va chizing. Hisob-kitoblar uchun TAU paketidagi dasturlardan foydalaning. Majburiy haqiqiy va xayoliy chastota javob qiymatlarini chop etish(10-15 ball mos keladi uchinchi va ikkinchi kvadrantlar).

4. Goldfarbning grafik-analitik usulidan foydalanib, barcha to'rtta rele uchun o'z-o'zidan tebranishlarning amplitudasi va chastotasini va ularning barqarorligini aniqlang. O'z-o'zidan tebranishlar parametrlarini analitik tarzda ham hisoblash mumkin. Har bir holat uchun tizimning fazaviy portretini sifat jihatidan tasvirlang.

5. Uch pozitsiyali rele uchun o'z-o'zidan tebranishlar bo'lmagan chiziqli qismning daromadining bir qiymatini va o'z-o'zidan tebranishlar muvaffaqiyatsizlikka uchragan chegara qiymatini aniqlang.

Eksperimental qism

1. Mavjud modellashtirish paketlaridan birini ishlatib, o'rganilayotgan ACP uchun modellashtirish sxemasini yig'ing. O'qituvchining ruxsati bilan siz tayyor sxemadan foydalanishingiz mumkin. O'chirish parametrlarini vazifaga muvofiq sozlang.

2. Kirishga x(t)=40*1(t) bosqichli harakatni qo‘llagan holda ideal rele (chop etish)li tizimdagi o‘tkinchi jarayonni o‘rganing. O'z-o'zidan tebranishlarning amplitudasi va chastotasini o'lchang, ularni hisoblangan qiymatlar bilan taqqoslang. Nolga teng bo'lmagan boshlang'ich shartlarni qo'yib, tajribani takrorlang (masalan, y(0)=10, y(1) (0)=-5).

3. Kirish signali amplitudasining ikki xil qiymati x(t)= 40*1(t) va x(t)=15*1(t) uchun uch pozitsiyali releli tizimdagi vaqtinchalik jarayonni oʻrganing. Vaqtinchalik jarayonlarni chop eting, o'z-o'zidan tebranishlarning amplitudasi va chastotasini o'lchang (agar ular mavjud bo'lsa), ularni hisoblangan qiymatlar bilan taqqoslang va xulosalar chiqaring.

4. Chiziqli qismning kuchayishining boshqa qiymatlari uchun uch pozitsiyali o'rni bo'lgan tizimdagi vaqtinchalik jarayonlarni o'rganing (5-bandning 3.1-bandiga qarang).

5. Nol va nolga teng bo'lmagan boshlang'ich sharoitlarda gistrezisi bo'lgan ikki pozitsiyali releli va x(t)=40*1(t) tizimdagi o'tkinchi jarayonlarni o'rganing. Vaqtinchalik jarayonlarni chop eting, o'z-o'zidan tebranishlarning amplitudasi va chastotasini o'lchang (agar ular mavjud bo'lsa), ularni hisoblangan qiymatlar bilan taqqoslang va xulosalar chiqaring.

Nazariy qism

Chiziqli bo'lmagan tizimlarni hisoblashda keng qo'llaniladigan usul garmonik linearizatsiya (funktsiyalarni tavsiflash) usuli hisoblanadi.

Usul o'z-o'zidan tebranishlarning parametrlarini (amplituda va chastota), o'z-o'zidan tebranishlarning barqarorligini va chiziqli bo'lmagan ASRning muvozanat holatining barqarorligini aniqlash imkonini beradi. Garmonik linearizatsiya usuli asosida vaqtinchalik jarayonlarni qurish, chiziqli bo'lmagan ASRni tahlil qilish va sintez qilish usullari ishlab chiqilgan.

Garmonik linearizatsiya usuli

Yuqorida aytib o'tilganidek, chiziqli bo'lmagan va ayniqsa releyli ASRlarda, barqaror davriy tebranishlar doimiy amplituda va chastota, deb ataladi o'z-o'zidan tebranishlar. Bundan tashqari, tizim parametrlarida sezilarli o'zgarishlar bo'lsa ham, o'z-o'zidan tebranishlar davom etishi mumkin. Amaliyot shuni ko'rsatdiki, ko'p hollarda boshqariladigan o'zgaruvchining tebranishlari (3-rasm) garmonikga yaqin.

O'z-o'zidan tebranishlarning garmoniklarga yaqinligi ularning parametrlarini - A amplitudasini va w 0 chastotasini aniqlash uchun garmonik linearizatsiya usulidan foydalanishga imkon beradi. Usul tizimning chiziqli qismi filtr ekanligi haqidagi taxminga asoslanadi past chastotalar(filtr gipotezasi). Keling, tizimdagi o'z-o'zidan tebranishlar garmonikga yaqin bo'lishi mumkin bo'lgan sharoitlarni aniqlaylik. Keling, rasmdagi kabi tizimlar bilan cheklanamiz. 3 chiziqli bo'lmagan element va chiziqli qismning ketma-ket ulanishiga qisqartirilishi mumkin. Oddiylik uchun mos yozuvlar signali doimiy qiymat deb faraz qilaylik, biz uni nolga tenglashtiramiz; Va xato signali (3-rasm) harmonik:

(1)

Chiziqli bo'lmagan elementning chiqish signali, har qanday davriy signal kabi - 3-rasmda bu to'rtburchaklar tebranishlar - Furye seriyasining harmonikalarining yig'indisi sifatida ifodalanishi mumkin.

Faraz qilaylik, tizimning chiziqli qismi past chastotali filtr (4-rasm) bo'lib, w 0 chastotali faqat birinchi garmonikadan o'tadi. 2w 0 va undan yuqori harmonik chastotali ikkinchisi chiziqli qism bilan filtrlanadi. Bunday holda, yoqilgan chiziqli chiqish qismlar faqat amalda mavjud bo'ladi birinchi garmonik , va yuqori harmoniklarning ta'sirini e'tiborsiz qoldirish mumkin

Shunday qilib, agar tizimning chiziqli qismi past chastotali filtr bo'lsa va o'z-o'zidan tebranishlar chastotasi w 0 shartlarni qondirsa.

, (4)

Tizimning chiziqli qismi past chastotali filtr degan taxmin deyiladi filtr gipotezasi . Filtr gipotezasi har doim qanoatlantiriladi, agar chiziqli qismning uzatish funktsiyasining maxraji va numeratorining ko'phadlari darajalari farqi bo'lsa.

(5)

kamida ikkita

Ko'pgina real tizimlar uchun shart (6) qoniqtiriladi. Masalan, ikkinchi tartibli aperiodik bog'lanish va haqiqiy integratsiya

. (7)

Garmonikaga yaqin o'z-o'zidan tebranishlarni o'rganishda chiziqli bo'lmagan elementning chiqishidagi davriy tebranishlarning faqat birinchi garmonikasi hisobga olinadi, chunki yuqori harmonikalar hali ham chiziqli qism tomonidan amalda filtrlanadi. O'z-o'zidan tebranish rejimida u amalga oshiriladi garmonik linearizatsiya chiziqli bo'lmagan element. Nochiziqli element bilan ekvivalent chiziqli element bilan almashtiriladi murakkab daromad (funktsiyani tavsiflovchi) kirish garmonik signalining amplitudasiga qarab:

qayerda va haqiqiy va xayoliy qismlar,

- argument,

- modul.

Umumiy holda, bu o'z-o'zidan tebranishlarning amplitudasi va chastotasiga ham, doimiy komponentga ham bog'liq. Chiziqli bo'lmagan elementning jismoniy jihatdan murakkab daromadi, ko'pincha deyiladi garmonik linearizatsiya koeffitsienti , Mavjud birinchi garmonikda chiziqli bo'lmagan elementning kompleks kuchayishi. Garmonik linearizatsiya koeffitsientining moduli

(9)

nochiziqli elementning chiqishidagi birinchi garmonik amplitudasining kirish garmonik signalining amplitudasiga nisbatiga son jihatdan teng.

Argument

(10)

chiqish tebranishlarining birinchi garmonikasi va kirish garmonik signali orasidagi faza siljishini tavsiflaydi. Aniq nochiziqliliklar uchun, masalan, rasmda. 2,a va 2,b, real ifoda va

Noaniq chiziqli bo'lmaganlar uchun, rasm. 2,c, 2,d, formula bilan aniqlanadi

bu erda S - histerezis halqasining maydoni. S maydoni, agar histerezis halqasi ijobiy yo'nalishda chetlab o'tilgan bo'lsa (2-rasm, s) va aks holda minus belgisi bilan (2-rasm, d) chetlab o'tilsa, ortiqcha belgisi bilan olinadi.

Umumiy holatda va formulalar yordamida hisoblab chiqiladi

, (12)

bu yerda , chiziqli bo‘lmagan funksiya (chiziqli bo‘lmagan elementning xarakteristikasi).

Yuqoridagilarni hisobga olgan holda, garmonikga yaqin o'z-o'zidan tebranishlarni o'rganishda chiziqli bo'lmagan ASR (3-rasm) chiziqli bo'lmagan element o'rniga garmonik chiziqlilanish koeffitsientiga ega ekvivalent bilan almashtiriladi (5-rasm). Rasmdagi chiziqli bo'lmagan elementning chiqish signali. 5 sifatida belgilangan, bu

chiziqli bo'lmagan element faqat hosil qilishini ta'kidlaydi

tebranishlarning birinchi garmonikasi. Odatdagi chiziqli bo'lmaganlar uchun garmonik linearizatsiya koeffitsientlari formulalarini adabiyotda topish mumkin, masalan. Ilova B-jadvalda o'rganilayotgan o'rni elementlarining xarakteristikalari, formulalar va ularning godograflari ko'rsatilgan. Ifodasi bilan aniqlangan teskari garmonik linearizatsiya koeffitsienti uchun formulalar va godograflar

, (13)

haqiqiy va xayoliy qismlar qayerda. Hodograflar va mos ravishda koordinatalarda va , va .

Keling, o'z-o'zidan tebranishlarning mavjudligi shartlarini yozamiz. Shakldagi tizim. 5 chiziqliga teng. Chiziqli tizimda, agar u barqarorlik chegarasida bo'lsa, so'rilmagan tebranishlar mavjud. Nyquist mezoniga muvofiq barqarorlik chegarasi shartidan foydalanamiz:

. (14)

Tenglama (14) Mavjud o'z-o'zidan tebranishlarning mavjudligi sharti, garmonikaga yaqin. Agar mavjud bo'lsa haqiqiy ijobiy (14) tenglamaning A va w 0 yechimlari, keyin chiziqli bo'lmagan ASRda garmonikga yaqin o'z-o'zidan tebranishlar mavjud. Aks holda, o'z-o'zidan tebranishlar yo'q yoki garmonik emas. Tenglama (14) ikkiga bo'linadi - haqiqiy va xayoliy qismlarga nisbatan:

;

(14) tenglamaning ikkala tomonini (13) formulaga bo'lib, L.S Goldfarb ko'rinishidagi o'z-o'zidan tebranishlarning mavjudligi shartini olamiz:

. (17)

(17) tenglama ham ikkiga bo'linadi:

(18)

ba'zi hollarda esa o'z-o'zidan tebranishlar parametrlarini aniqlash uchun ulardan foydalanish qulayroqdir.

Goldfarb (17) tizimni yechish va o'z-o'zidan tebranishlar barqarorligini aniqlashning grafik-analitik usulini taklif qildi.

Koordinatalarda , va , godograflar va quriladi (6-rasm, a). Agar godograflar kesishsa, u holda o'z-o'zidan tebranishlar mavjud. O'z-o'zidan tebranishlarning parametrlari - A va w 0 kesishish nuqtalarida aniqlanadi - chastota w 0 hodograf bo'yicha, amplituda godograf bo'yicha. Shaklda. 6,a - ikkita chegara davri mavjudligini ko'rsatadigan ikkita kesishish nuqtasi.

O'z-o'zidan tebranishlarning barqarorligini aniqlash uchun Goldfarbning fikriga ko'ra, chastotani oshirish yo'nalishi bo'yicha OFK bo'ylab harakatlanayotganda chiziqli qismning AFC chap tomoni soyalanadi (6-rasm).

O'z-o'zidan tebranishlar barqaror bo'ladi, agar kesishish nuqtasida chiziqli bo'lmagan elementning godografi A amplitudasining ortishi yo'nalishi bo'yicha harakatlanayotganda soyasiz maydondan soyali maydonga o'tsa.

Agar soyali maydondan soyasiz joyga o'tish sodir bo'lsa, u holda o'z-o'zidan tebranishlar barqaror emas.

Shaklda. Shakl 6b, shakldagi ikkita chegara davriga mos keladigan fazali portretni sifat jihatidan tasvirlaydi. 6, a. Parametrlar bilan kesishish nuqtasi va rasmda. 6a shakldagi beqaror chegara davriga mos keladi. 6b, parametrlar bilan ishora qiling va o'z-o'zidan tebranishlarning buzilishiga erishish uchun, bu holda hodograflar va kesishmang. Xuddi shu ta'sirga o'lik zonani oshirish yoki B relesining chiqish signalining amplitudasini kamaytirish orqali erishish mumkin. Xato! Aloqa xatosi. xuddi o'sha payt , va amplituda qiymati. Tabiiyki, bu tizimning fazaviy portretini sifat jihatidan o'zgartirishga olib keladi.

O'z-o'zidan tebranishlarning garmoniklarga yaqinligi ularning parametrlarini - A amplitudasini va w 0 chastotasini aniqlash uchun garmonik linearizatsiya usulidan foydalanishga imkon beradi. Usul tizimning chiziqli qismi past chastotali filtr (filtr gipotezasi) degan taxminga asoslanadi. Keling, tizimdagi o'z-o'zidan tebranishlar garmonikga yaqin bo'lishi mumkin bo'lgan sharoitlarni aniqlaylik. Keling, rasmdagi kabi tizimlar bilan cheklanamiz. 3 chiziqli bo'lmagan element va chiziqli qismning ketma-ket ulanishiga qisqartirilishi mumkin. Oddiylik uchun mos yozuvlar signali doimiy qiymat deb faraz qilaylik, biz uni nolga tenglashtiramiz; Va xato signali (3-rasm) harmonik:

Shunday qilib, agar tizimning chiziqli qismi past chastotali filtr bo'lsa va o'z-o'zidan tebranishlar chastotasi w 0 shartlarni qondirsa.

, (4)

kamida ikkita

Ko'pgina real tizimlar uchun shart (6) qoniqtiriladi. Masalan, ikkinchi tartibli aperiodik bog'lanish va haqiqiy integratsiya

qayerda va haqiqiy va xayoliy qismlar,

- argument,

- modul.

nochiziqli elementning chiqishidagi birinchi garmonik amplitudasining kirish garmonik signalining amplitudasiga nisbatiga son jihatdan teng.

Argument

chiqish tebranishlarining birinchi garmonikasi va kirish garmonik signali orasidagi faza siljishini tavsiflaydi. Aniq nochiziqliliklar uchun, masalan, rasmda. 2,a va 2,b, real ifoda va

Noaniq chiziqli bo'lmaganlar uchun, rasm. 2,c, 2,d, formula bilan aniqlanadi

Umumiy holatda va formulalar yordamida hisoblab chiqiladi

bu yerda , chiziqli bo‘lmagan funksiya (chiziqli bo‘lmagan elementning xarakteristikasi).

Chiziqli bo'lmagan element faqat hosil qilishini ta'kidlaydi

haqiqiy va xayoliy qismlar qayerda. Hodograflar va mos ravishda koordinatalarda va , va .

Garmonik linearizatsiya usuli chiziqli tizimlar uchun ishlab chiqilgan usullardan foydalangan holda amaliyot uchun etarli darajada aniqlik bilan chiziqli bo'lmagan tizimlarning barqarorligi va aniqligini o'rganish imkonini beradi. Usul o'z-o'zidan tebranishlarning mavjudligini, shuningdek ularning chastotasi va amplitudasini aniqlash imkonini beradi.

Chiziqli bo'lmagan tizim chiziqli va chiziqli bo'lmagan qismlarning ulanishi sifatida ifodalanadi (5-rasm).

Guruch. 5 Nochiziqli tizim diagrammasi

Tizimning chiziqli bo'lmagan qismining chiqish signali odatda ifoda bilan aniqlanadi

Chiziqli qismning uzatish funksiyasi sifatida belgilaymiz. Tenglamalar tizimi shaklni oladi

Tizimning chiziqli qismining chiqishida shaklning garmonik tebranishlari paydo bo'ladigan sharoitlarni topamiz.

Bu holda signal y(t) chiziqli bo'lmagan qism ham ifodalaydi davriy funktsiya, lekin sinusoiddan farq qiladi. Ushbu funktsiyani Furye seriyasiga kengaytirish mumkin

Ushbu ifodada a i Va b i- Furye koeffitsientlari. Simmetrik nochiziqliliklar uchun F 0 =0.

Usul tizimning chiziqli qismiga qo'yadigan asosiy shart - bu past o'tkazuvchan filtr holati. Chiziqli qism faqat tebranishlarning birinchi garmonikasini uzatadi, deb ishoniladi. Bu taxmin (7.19) dagi yuqori harmonikalarni ahamiyatsiz deb hisoblashimizga imkon beradi va signalning faqat birinchi harmonikasini hisobga olish bilan cheklanadi. y(t).

keyin (7.20) ifodani shunday qayta yozish mumkin

(7.17) sistemaning birinchi tenglamasi shaklni oladi

Ushbu ifodada

Nonlineerlikni almashtirish natijasi F(x,sx) ifoda

va garmonik linearizatsiya deyiladi. Miqdorlar q Va q 1 garmonik linearizatsiya koeffitsientlari yoki oddiygina garmonik koeffitsientlar deyiladi. Bir qiymatli nochiziqlilar uchun odatda shunday bo'ladi q 1 =0 . Tipik nochiziqliliklarga mos keladigan garmonik koeffitsientlar uchun formulalar ilovalarda keltirilgan.

Garmonik linearizatsiya va an'anaviy linearizatsiya o'rtasidagi tub farq shundaki, an'anaviy linearizatsiya bilan chiziqli bo'lmagan xarakteristikalar ma'lum bir doimiy qiyalik bilan to'g'ri chiziq bilan almashtiriladi va garmonik linearizatsiya bilan - qiyaligi kirish amplitudasiga bog'liq bo'lgan to'g'ri chiziq bilan almashtiriladi. chiziqli bo'lmagan elementning signali.

Keling, o'z-o'zidan tebranishlarning amplitudasi va chastotasini aniqlash texnikasini ko'rib chiqaylik.

1). (7.22) dan olingan sistemaning xarakteristik tenglamasida almashtirishni amalga oshiramiz s=j va olamiz

2). Olingan ifodadan biz haqiqiy va xayoliy qismlarni tanlaymiz va ularni nolga tenglashtiramiz, bu Mixaylov mezoniga ko'ra, tebranish barqarorligi chegarasida joylashgan tizimga mos keladi.

3).Ushbu tizimni yechish garmonik koeffitsientlarning chastotasi va qiymatlarini beradi. Agar bu qiymatlar haqiqiy va ijobiy bo'lsa, u holda tizim chegara aylanishiga ega. Garmonik koeffitsientlarning qiymatlaridan chegara tsiklining amplitudasini aniqlash mumkin.
4). Cheklangan tsiklning barqarorligining umumiy belgisi, ya'ni. O'z-o'zidan tebranishlarning mavjudligi chegara siklining amplitudasi va chastotasining olingan qiymatlarida oxirgidan oldingi Hurvits determinantining nolga tengligi. Ko'pincha Mixaylov barqarorlik mezoniga asoslangan chegara davrining barqarorligi shartidan foydalanish qulayroqdir.

Agar bu tengsizlik qanoatlantirilsa, u holda chegara davri barqaror bo'ladi va tizimda yuqorida aniqlangan amplituda va chastota bilan o'z-o'zidan tebranishlar mavjud. “*” indeksi lotinlar qachon hisoblanganligini bildiradi ma'lum qiymatlar garmonik koeffitsientlar, amplituda va chastota.

Misol. Faraz qilaylik, yuqorida muhokama qilingan samolyotning burchak burchagini barqarorlashtirish tizimida rul boshqaruvi chiziqli bo'lmagan va uning strukturaviy diagrammasi rasmda ko'rsatilgan shaklga ega. 7.6.

6-rasm Rulda boshqaruvining chiziqli bo'lmagan sxemasi

Rulda chalg'igan tezligi xususiyatlarining chiziqli bo'lmaganligi uchun quyidagi parametrlarni o'rnatamiz: b = 0,12, k 1 = tg =c/b = 6,7. Ushbu nochiziqlilikning garmonik linearizatsiya koeffitsientlari ifodalar bilan aniqlanadi

Zanjirdagi chiziqli bo'lmagan xarakteristikani harmonik koeffitsient bilan almashtirib, biz rul haydovchisining uzatish funktsiyasini olamiz.

Keling, bu uzatish funktsiyasini qadam burchagi barqarorligi tizimining blok diagrammasiga almashtiramiz va uzatish funktsiyasini aniqlaymiz. yopiq tizim

Yopiq tizimning xarakteristik tenglamasida biz almashtirishni amalga oshiramiz s = j va haqiqiy va xayoliy qismlarni tanlang.

Tizimning ikkinchi tenglamasidan biz chastota ifodasini olamiz: va uni birinchi tenglamaga almashtirib, transformatsiyalardan so'ng biz olamiz.

Bu erda xarakterli tenglamaning koeffitsientlari uchun oldindan aniqlangan ifodalarni almashtirib, biz garmonik koeffitsient uchun kvadrat tenglamani olishimiz mumkin, uni yechish orqali biz topamiz.

Ushbu qiymatlardan foydalanib, siz ikkita holat uchun xarakterli tenglamaning barcha koeffitsientlarini hisoblashingiz va har bir qiymatga mos keladigan chastotalarni aniqlashingiz mumkin. q(A). Biz olamiz:

Harmonik koeffitsientning ikkala qiymati ham, mos keladigan chastotalar ham haqiqiy va ijobiydir. Shunday qilib, tizimda ikkita chegara davri mavjud. Cheklangan tsiklning amplituda qiymatlari harmonik linearizatsiya koeffitsienti formulasi oldindan hisoblangan qiymatga teng bo'lgan qiymatni tanlash orqali raqamli aniqlanadi. Ko'rib chiqilayotgan holatda biz olamiz

Endi chegara davrlarining barqarorligini baholaylik. Biz Mixaylov mezonidan olingan tengsizlikdan foydalanamiz, buning uchun biz aniqlaymiz

Olingan ifodalarga kiritilgan garmonik chiziqlilanish koeffitsientining hosilasi formula yordamida hisoblanadi

Yuqoridagi formulalar yordamida hisob-kitoblar shuni ko'rsatadiki, birinchi chegara davri barqaror emas va u qachon sodir bo'ladi (0) 0.1166(6.7 0 ). Agar boshlang'ich og'ish belgilanganidan kam bo'lsa, unda chiziqli bo'lmagan elementning kirishidagi jarayon namlanadi (7. 7-rasm) va tizim barqaror.

Agar qadam burchagining boshlang'ich qiymati belgilanganidan katta bo'lsa, u holda jarayonlar barqaror bo'lgan ikkinchi chegara davriga yaqinlashadi va shuning uchun tizimda o'z-o'zidan tebranishlar paydo bo'ladi (8-rasm).

Guruch. 8

Modellashtirish orqali barqaror chegara siklining tortishish hududi taxminan chegaralar ichida ekanligi aniqlandi. (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).

samarapedsovet.ru