Metoda harmonijske linearizacije: Upute za laboratorijski rad. Harmonijska linearizacija Koeficijenti harmonijske linearizacije

14.08.2021

Ministarstvo obrazovanja i znanosti Ruske Federacije

Saratovsko državno tehničko sveučilište

Balakovo Institut za inženjerstvo, tehnologiju i menadžment

Metoda harmonijske linearizacije

Smjernice za laboratorijski rad u kolegiju “Teorija automatskog upravljanja” za studente specijalnosti 210100

Odobreno

urednički i izdavački savjet

Tehnološki institut Balakovo,

tehnologija i menadžment

Balakovo 2004

Svrha rada: Proučavanje nelinearnih sustava metodom harmonijske linearizacije (harmonijske ravnoteže), određivanje koeficijenata harmonijske linearizacije za različite nelinearne veze. Stjecanje vještina u pronalaženju parametara simetričnih oscilacija konstantne amplitude i frekvencije (autooscilacija), korištenjem algebarskih, frekvencijskih metoda, te korištenjem Mihajlovljevog kriterija.

OSNOVNE INFORMACIJE

Metoda harmonijske linearizacije odnosi se na približne metode proučavanja nelinearnih sustava. Omogućuje vrlo jednostavnu i s prihvatljivom točnošću procjenu stabilnosti nelinearnih sustava i određivanje frekvencije i amplitude oscilacija uspostavljenih u sustavu.

Pretpostavlja se da se nelinearni ACS koji se proučava može prikazati u sljedećem obliku

a nelinearni dio mora imati jednu nelinearnost

. (1)

Ova nelinearnost može biti kontinuirana ili relejna, jednostruka ili histerezična.

Bilo koja funkcija ili signal može se proširiti u niz prema sustavu linearno neovisnih, u određenom slučaju, ortonormiranih funkcija. Kao takav ortogonalni red može se koristiti Fourierov red.

Proširimo izlazni signal nelinearnog dijela sustava u Fourierov red

, (2)

ovdje su Fourierovi koeficijenti,

. (3)

Dakle, signal prema (2) može se prikazati kao beskonačna suma harmonika s rastućim frekvencijama itd. Ovaj signal se dovodi na ulaz linearnog dijela nelinearnog sustava.

Označimo prijenosnu funkciju linearnog dijela

, (4)

a stupanj polinoma brojnika mora biti manji od stupnja polinoma nazivnika. U ovom slučaju, frekvencijski odziv linearnog dijela ima oblik

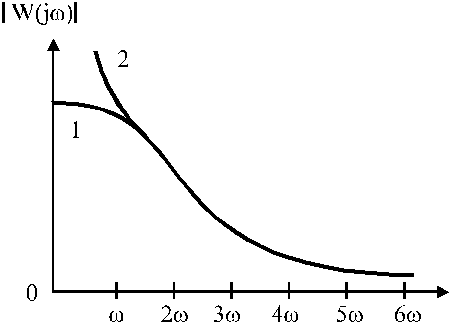
gdje 1 - nema polova, 2 - ima pol ili polove.

Za frekvencijski odziv pošteno je napisati

Dakle, linearni dio nelinearnog sustava je visokopropusni filtar. U tom će slučaju linearni dio prenositi samo niske frekvencije bez prigušenja, dok će visoke frekvencije biti značajno prigušene kako frekvencija raste.

Kod metode harmonijske linearizacije pretpostavlja se da će linearni dio sustava propuštati samo istosmjernu komponentu signala i prvi harmonik. Tada će signal na izlazu linearnog dijela imati oblik

Ovaj signal prolazi kroz cijeli zatvoreni krug sustava sl. 1 i na izlazu nelinearnog elementa bez uzimanja u obzir viših harmonika, prema (2) imamo

. (7)

Pri proučavanju nelinearnih sustava metodom harmonijske linearizacije mogući su slučajevi simetričnih i nesimetričnih oscilacija. Razmotrimo slučaj simetričnih oscilacija. Ovdje i.

Uvedimo sljedeću oznaku

Zamjenjujući ih u (7), dobivamo . (8)

S obzirom na to

, Gdje ,

. (9)

Prema (3) i (8) kada

. (10)

Izraz (9) je harmonijska linearizacija nelinearnosti uspostavlja linearni odnos između ulazne varijable i izlazne varijable na . Veličine i nazivaju se koeficijenti harmonijske linearizacije.

Treba napomenuti da je jednadžba (9) linearna za određene veličine i (amplitudu i frekvenciju harmonijskih oscilacija u sustavu). Ali općenito, zadržava nelinearna svojstva, budući da su koeficijenti različiti za različite i . Ova nam značajka omogućuje proučavanje svojstava nelinearnih sustava pomoću metode harmonijske linearizacije [Popov E.P.].

U slučaju asimetričnih oscilacija, harmonijska linearizacija nelinearnosti dovodi do linearne jednadžbe

. (12)

Kao i jednadžba (9), linearizirana jednadžba (11) zadržava svojstva nelinearnog elementa, budući da koeficijenti harmonijske linearizacije , , kao i konstantna komponenta ovise i o pomaku i amplitudi harmonijskih oscilacija.

Jednadžbe (9) i (11) omogućuju nam dobivanje prijenosnih funkcija harmonijski lineariziranih nelinearnih elemenata. Dakle, za simetrične vibracije

U ovom će se poglavlju prikazati metoda harmonijske linearizacije za približno određivanje periodičkih rješenja (autooscilacija) i stabilnosti nelinearnih sustava bilo kojeg reda, koja je po ideji bliska metodi ekvivalentne linearizacije ili metodi harmonijske ravnoteže N. M. Krylova i N. N. Bogolyubov, a prema rezultatima - i na metodu malih parametara B. V. Bulgakova.

Približna metoda koja se razmatra moćan je alat za proučavanje nelinearnih automatskih sustava u smislu jednostavnosti i prilično visoke svestranosti njezine aparature kada se primijeni na široku lepezu nelinearnosti. Međutim, treba imati na umu da to približno rješava problem. Postoje određena ograničenja njegove primjenjivosti, o čemu će biti riječi u nastavku. Ta se ograničenja obično dobro promatraju u problemima teorije automatskog upravljanja. Praktični proračuni i eksperiment pokazuju prihvatljivost ove metode za mnoge vrste nelinearnih sustava.

Neka je dan neki nelinearni izraz forme

Proširujući funkciju s desne strane izraza (18.1) u Fourierov red, dobivamo

što znači nepostojanje konstantne komponente u ovoj ekspanziji. U ovom poglavlju, pretpostavlja se da je zadovoljen uvjet za odsutnost konstantne komponente (18.5). Naknadno će (poglavlje 19) biti dana metoda proučavanja samooscilacija u prisutnosti konstantne komponente, odnosno u slučaju neispunjenja uvjeta (18.5).

Ako uzmemo u obzir da iz (18.2) i (18.3)

tada se formula (18.4) pod uvjetom (18.5) može napisati u obliku

gdje su q harmonijski koeficijenti linearizacije, određeni formulama:

Dakle, nelinearni izraz (18.1) na zamijenjen je izrazom (18.6), koji je sličan linearnom do viših harmonika. Ova se operacija naziva harmonijska linearizacija. Koeficijenti su konstantni pri konstantnim vrijednostima, tj. u slučaju periodičkog procesa. U prijelaznom oscilatornom procesu, s promjenom a i co, mijenjaju se koeficijenti q i (vidi poglavlje 20). Za različite amplitude i frekvencije periodičkih procesa, koeficijenti izraza (18.6) bit će različiti po veličini. Ova okolnost, koja je vrlo važna za daljnju raspravu, je značajna razlika između harmonijske linearizacije, u usporedbi s uobičajenom metodom linearizacije (§ 3.1), što dovodi do čisto linearnih izraza koji su korišteni u prethodnim odjeljcima knjige. Ova će okolnost omogućiti, primjenom linearnih metoda istraživanja na izraz (18.6), analizu osnovnih svojstava nelinearnih sustava koja se ne mogu otkriti konvencionalnom linearizacijom.

Također predstavljamo harmonijske linearizacijske formule za jednostavniju nelinearnost:

Ovdje postoje dvije mogućnosti: 1) krivulja ima petlju histereze (na primjer, sl. 16.18, c, sl. 16.22, d, e), i 2) krivulja nema petlju histereze (sl. 16.8, b , sl. 16.22, a itd.).

U prisutnosti petlje histereze, kada se zapravo promatra ovisnost o predznaku derivata, nelinearna funkcija nakon harmonijske linearizacije zamjenjuje se sljedećim izrazom (sa

pod uvjetom da nema konstantne komponente:

Ako krivulja nema petlju histereze, tada će biti

(s petljom histereze, ovaj integral nije bio nula zbog razlike u obrisu krivulje tijekom povećanja i pada

Posljedično, u nedostatku petlje histereze, nelinearni izraz (18.8) zamjenjuje se jednostavnijim:

tj. krivocrtna ili izlomljena karakteristika, točna na više harmonike, zamjenjuje se pravocrtnom, čiji nagib q ovisi o veličini amplitude titranja a. Drugim riječima, nelinearna veza se uspoređuje s "linearnom" s prijenosnim omjerom (pojačanjem) koji ovisi o amplitudi a oscilacija ulazne veličine x.

Prema (18.9), petlja histereze uvodi, dodatno, derivat koji daje fazno kašnjenje, budući da se, dakle, nelinearno koordinatno kašnjenje u obliku petlje histereze pretvara u ekvivalentno linearno fazno kašnjenje tijekom harmonijske linearizacije.

Moguće je stvoriti posebnu nelinearnu vezu s vodećom petljom, koja će biti ekvivalentna linearnom faznom pomaku pri uvođenju derivacije, ali s tom razlikom da će veličina faznog pomaka ovisiti o veličini amplitude titranja, koja to nije slučaj u linearnim sustavima.

U slučajevima kada je nelinearna veza opisana složenom jednadžbom koja uključuje zbroj različitih linearnih i nelinearnih izraza, svaki od nelinearnih članova zasebno se podvrgava harmonijskoj linearizaciji. Umnožak nelinearnosti nužno se u cjelini promatra kao jedna složena nelinearnost. U tom slučaju mogu se pojaviti nelinearne funkcije različite prirode.

Na primjer, s harmoničnom linearizacijom druge jednadžbe (16.3), morat ćete se pozabaviti funkcijom na . U ovom slučaju dobivamo

s obzirom na to

Ako je funkcija ili funkcija jedina nelinearna funkcija u jednadžbi nelinearne veze, onda s harmonijskom

linearizaciju možemo staviti i

slično prethodnim formulama (18.6) i (18.7). Ali u ovom slučaju, vrijednost a u svim izračunima bit će amplituda fluktuacija brzine, a ne sama x koordinata. Potonji će tada imati amplitudu

Pri izračunavanju koeficijenata harmonijske linearizacije pomoću formula (18.10) treba imati na umu da se za simetrične nelinearne karakteristike integral može dobiti udvostručenjem integrala, tj.

a za karakteristike bez histereze simetrične s obzirom na ishodište koordinata pri proračunu, može se napisati

Navedimo izraze za koeficijente nekih od najjednostavnijih nelinearnih veza. Zatim se mogu izravno koristiti za rješavanje različitih specifičnih problema.

Koeficijenti harmonijske linearizacije relejnih veza. Nađimo koeficijente i jednadžbe najtipičnijih relejnih veza pomoću formula (18.10). Pogledajmo općenito karakteristike relejne veze prikazane grafikonom na sl. 18.1, a, gdje ga ima razlomački broj u intervalu

Kao posebni slučajevi dobit će se jednadžbe ostalih vrsta relejnih veza.

Ako oscilacije ulazne veličine imaju amplitudu, tada prema sl. 18.1, ali neće biti pomaka u sustavu. Ako je amplituda tada se relejni prekidači javljaju u točkama A, B, C, D (Sl. 18.1, b), na kojima imamo

Posljedično, nakon korištenja svojstava, svaki od integrala (18.10) dijeli se na tri člana:

a prvi i treći od njih prema sl. 18.1, i i bit će nule. Stoga izrazi (18.10) imaju oblik

i jednadžba relejne veze s karakteristikom kao na sl. 18.1, ali će imati oblik (18.9) s vrijednostima i dobivenim ovdje.

Razmotrimo posebne slučajeve.

Za relejnu vezu s karakteristikom bez histerezne petlje, ali s mrtvom zonom (Sl. 18.1, a), pretpostavljajući iz gornjih formula dobivamo

Za karakteristiku releja s petljom histereze kao što je sl. pod pretpostavkom da imamo

Konačno, za idealnu relejnu vezu (Sl. 18.1, e), pod pretpostavkom da nađemo

U posljednjem primjeru lako je vidjeti smisao harmonijske linearizacije karakteristike releja. Pisani izraz za q znači zamjenu izlomljene linije ravnom linijom (slika 18.1, e) s takvim nagibom da ta ravna linija približno zamjenjuje dio izlomljene linije koji je pokriven zadanom amplitudom a. Odavde postaje sasvim jasno proporcionalna ovisnost od a, dano formulom (18.18), budući da je veća amplituda a oscilacija ulazne vrijednosti, to bi ravna linija trebala biti ravnija, približno zamjenjujući izlomljenu liniju

Slična je situacija i s karakteristikom releja na sl. 18.1, d za koji je nagib ravne crte koja ga zamjenjuje dan formulom (18.16). Posljedično, svaka relejna veza bez histereze u oscilatornom procesu ekvivalentna je takvoj "linearnoj" vezi čiji prijenosni omjer (pojačanje) opada s povećanjem amplitude oscilacija ulazne veličine, počevši od

Što se tiče relejne veze s petljom histereze, prema (18.9) i (18.17), ona se zamjenjuje linearnom vezom s pojačanjem sličnim prethodnom, ali uz to, uz uvođenje negativne derivacije na desna strana jednadžbe. Uvođenje negativne derivacije za razliku od pozitivne (vidi § 10.2) uvodi fazni odmak u odgovoru veze na radnju unosa. Ovo služi kao "linearni ekvivalent" zamjenjujući učinak nelinearnosti u obliku petlje histereze. pri čemu

koeficijent derivacije prema (18.17) također opada s povećanjem amplitude a oscilacija ulazne veličine, što je i razumljivo, jer bi učinak utjecaja petlje histereze na proces oscilacija u relejnom linku trebao biti manji, veća je amplituda oscilacija u odnosu na širinu petlje histereze.

Koeficijenti harmonijske linearizacije ostalih najjednostavnijih nelinearnih veza. Razmotrimo nelinearnu vezu s mrtvom zonom i zasićenjem (slika 18.2, a). Prema sl. 18.2, b, gdje

integral (18.10) u odjeljku je podijeljen na pet članova, od kojih su dva jednaka nuli. Zato

gdje sa zamjenom dobivamo

gdje su određeni formulama (18.19). Zbog nepostojanja petlje histereze ovdje

Dakle, jednadžba nelinearne veze s karakteristikom kao na Sl. 18.2, a gdje će biti određeno izrazom (18.20).

Kao poseban slučaj, ovo daje vrijednost za vezu s mrtvom zonom bez zasićenja (Sl. 18.2, c). Da bismo to učinili, u prethodnom rješenju moramo staviti i, prema tome, Zatim

Kao što vidimo, poveznica s mrtvom zonom ovdje se uspoređuje s linearnom vezom s pojačanjem smanjenim zbog toga. Ovo smanjenje pojačanja je značajno pri malim amplitudama i malo pri velikim, i pri

Uvod

Relejni sustavi postali su široko rasprostranjeni u praksi automatskog upravljanja. Prednost relejnih sustava je njihova jednostavnost dizajna, pouzdanost, jednostavnost održavanja i konfiguracije. Relejni sustavi predstavljaju posebnu klasu nelinearnih sustava automatskog upravljanja.

Za razliku od kontinuiranih u relejnim sustavima, regulatorno djelovanje se naglo mijenja kad god upravljački signal releja (najčešće je to pogreška upravljanja) prođe kroz neke fiksne (pražne) vrijednosti, na primjer, kroz nulu.

Relejni sustavi u pravilu imaju visoke performanse zbog činjenice da se upravljačko djelovanje u njima mijenja gotovo trenutno, a aktuator je izložen konstantnom signalu maksimalne amplitude. Istodobno, u relejnim sustavima često se javljaju samooscilacije, što je u mnogim slučajevima nedostatak. U ovom radu proučavan je relejni sustav s četiri različita zakona upravljanja.

Struktura proučavanog sustava

Proučavani sustav (slika) 1 uključuje usporedni element ES, relejni element RE, aktuator (idealni integrator s pojačanjem = 1), upravljački objekt (aperiodična veza s tri vremenske konstante , , i pojačanje). Vrijednosti parametara sustava dane su u tablici. 1 Dodatak A.

Statičke karakteristike (ulazno-izlazne karakteristike) relejnih elemenata koji se proučavaju prikazane su na sl. 2.

Na sl. 2a prikazuje karakteristike idealnog releja s dva položaja, sl. 2b karakteristika releja s tri položaja s mrtvom zonom. Na sl. 2,c i 2,d prikazuju karakteristike dvopoložajnog releja s pozitivnom odnosno negativnom histerezom.

Istraživani ASR može se modelirati korištenjem dobro poznatih paketa za modeliranje, na primjer, SIAM ili VisSim.

Komentar. U nekim simulacijskim paketima izlazna vrijednost

signal releja može uzeti samo vrijednosti ±1 umjesto ±B, gdje je B proizvoljan broj. U takvim slučajevima potrebno je uzeti dobitak integratora jednak .

Radni nalog

Za dovršetak rada svaki učenik od nastavnika dobiva verziju početnih podataka (vidi odjeljak 2).

Radovi se izvode u dvije faze.

Prva faza je računska i istraživačka (može se izvoditi izvan laboratorija).

Druga faza je eksperimentalna (provodi se u laboratoriju). U ovoj fazi, pomoću jednog od paketa, simuliraju se prijelazni procesi u sustavu koji se proučava za modove izračunate u prvoj fazi, te se provjerava točnost teorijskih metoda.

Potreban teorijski materijal prikazan je u odjeljku 4; Odjeljak 5 sadrži ispitna pitanja.

3.1. Računski i istraživački dio

1. Dobiti izraze za amplitudno-frekvencijske i fazno-frekvencijske, realne i imaginarne karakteristike linearnog dijela sustava.

2. Izračunati i konstruirati amplitudno-faznu karakteristiku linearnog dijela sustava. Za izračune koristiti programe iz TAU paketa. Obavezno ispisati stvarne i imaginarne vrijednosti frekvencijskog odziva(odgovara 10 – 15 bodova treći i drugi kvadranti).

4. Goldfarbovom grafičko-analitičkom metodom odrediti amplitudu i frekvenciju vlastitih oscilacija te njihovu stabilnost za sva četiri releja. Parametri autooscilacija mogu se izračunati i analitički. Kvalitativno prikazati fazni portret sustava za svaki slučaj.

5. Za tropoložajni relej odrediti jednu vrijednost pojačanja linearnog dijela kod koje nema autooscilacija, te graničnu vrijednost pri kojoj autooscilacije nestaju.

eksperimentalni dio

1. Koristeći jedan od dostupnih paketa za modeliranje, sastavite shemu modeliranja za ASR koji se proučava. Uz dopuštenje učitelja, možete koristiti gotov dijagram. Konfigurirajte parametre kruga u skladu sa zadatkom.

2. Istražite prijelazni proces u sustavu s idealnim relejem (ispišite ga), primjenjujući postupno djelovanje x(t)=40*1(t) na ulaz. Izmjerite amplitudu i frekvenciju vlastitih oscilacija, uspoređujući ih s izračunatim vrijednostima. Ponovite eksperiment, postavljajući početne uvjete različite od nule (na primjer, y(0)=10, y(1) (0)=-5).

3. Istražite prijelazni proces u sustavu s tropozicijskim relejem za dvije različite vrijednosti amplitude ulaznog signala x(t)= 40*1(t) i x(t)=15*1(t). Ispiši prijelazne procese, izmjeri amplitudu i frekvenciju autooscilacija (ako postoje), usporedi ih s izračunatim vrijednostima i izvedi zaključke.

4. Istražite prijelazne procese u sustavu s relejem s tri položaja za druge vrijednosti dobitka linearnog dijela (vidi paragraf 5, odjeljak 3.1).

5. Istražiti prijelazne procese u sustavu s dvopoložajnim relejima s histerezom pri nultim i nenultim početnim uvjetima i x(t)=40*1(t). Ispiši prijelazne procese, izmjeri amplitudu i frekvenciju autooscilacija (ako postoje), usporedi ih s izračunatim vrijednostima i izvedi zaključke.

Teorijski dio

Široko korištena metoda za proračun nelinearnih sustava je metoda harmonijske linearizacije (opisivanje funkcija).

Metoda omogućuje određivanje parametara autooscilacija (amplituda i frekvencija), stabilnosti autooscilacija i stabilnosti ravnotežnog položaja nelinearnog ASR. Na temelju metode harmonijske linearizacije razvijene su metode za konstruiranje prijelaznih procesa, analizu i sintezu nelinearnih ASR.

Metoda harmonijske linearizacije

Kao što je već navedeno, u nelinearnim i posebno relejnim ASR-ovima, stabilne periodične oscilacije konstantne amplitude i frekvencije, tzv samooscilacije. Štoviše, samooscilacije mogu postojati čak i uz značajne promjene parametara sustava. Praksa je pokazala da su u mnogim slučajevima oscilacije regulirane veličine (slika 3) bliske harmoničkim.

Blizina vlastitih oscilacija harmoničkim omogućuje nam korištenje metode harmonijske linearizacije za određivanje njihovih parametara - amplitude A i frekvencije w 0. Metoda se temelji na pretpostavci da je linearni dio sustava filtar niske frekvencije(hipoteza filtera). Odredimo uvjete pod kojima samooscilacije u sustavu mogu biti bliske harmoničkim. Ograničimo se na sustave koji, kao na Sl. 3 može se svesti na serijski spoj nelinearnog elementa i linearnog dijela. Pretpostavimo da je referentni signal konstantna vrijednost, radi jednostavnosti, uzet ćemo ga jednak nuli. A signal greške (slika 3) je harmoničan:

(1)

Izlazni signal nelinearnog elementa, kao i svaki periodički signal - na slici 3 su to pravokutne oscilacije - može se prikazati kao zbroj harmonika Fourierovog reda.

Pretpostavimo da je linearni dio sustava niskopropusni filtar (slika 4) i da propušta samo prvi harmonik s frekvencijom w 0. Drugi s frekvencijom od 2w 0 i višim harmonicima filtrira se linearnim dijelom. U ovom slučaju, na linearni izlaz dijelovi će postojati praktički samo prvi harmonik , a utjecaj viših harmonika može se zanemariti

Dakle, ako je linearni dio sustava niskopropusni filtar, a frekvencija samooscilacija w 0 zadovoljava uvjete

, (4)

Pretpostavka da je linearni dio sustava niskopropusni filtar tzv hipoteza filtera . Hipoteza filtra uvijek je zadovoljena ako je razlika u stupnjevima polinoma nazivnika i brojnika prijenosne funkcije linearnog dijela

(5)

barem dva

Uvjet (6) je zadovoljen za mnoge realne sustave. Primjer je aperiodična veza drugog reda i realna integracija

. (7)

Pri proučavanju samooscilacija bliskih harmoničkim, uzima se u obzir samo prvi harmonik periodičnih oscilacija na izlazu nelinearnog elementa, budući da se viši harmonici još uvijek praktički filtriraju linearnim dijelom. U režimu samooscilacije se provodi harmonijska linearizacija nelinearni element. Nelinearni element zamjenjuje se ekvivalentnim linearnim s složeni dobitak (opisna funkcija) ovisno o amplitudi ulaznog harmonijskog signala:

gdje su i gdje su stvarni i imaginarni dijelovi,

– argument,

– modul.

U općem slučaju ovisi i o amplitudi i frekvenciji vlastitih oscilacija i o konstantnoj komponenti. Fizički složeno pojačanje nelinearnog elementa, češće se naziva koeficijent harmonijske linearizacije , Tamo je kompleksno pojačanje nelinearnog elementa na prvom harmoniku. Modul harmonijskog koeficijenta linearizacije

(9)

brojčano je jednaka omjeru amplitude prvog harmonika na izlazu nelinearnog elementa i amplitude ulaznog harmoničkog signala.

Argument

(10)

karakterizira fazni pomak između prvog harmonika izlaznih oscilacija i ulaznog harmonijskog signala. Za nedvosmislene nelinearnosti, kao što je, na primjer, na Sl. 2,a i 2,b, realni izraz i

Za dvosmislene nelinearnosti, Sl. 2,c, 2,d, određeno formulom

gdje je S područje petlje histereze. Područje S uzima se s predznakom plus ako se petlja histereze zaobilazi u pozitivnom smjeru (slika 2, c) i s predznakom minus u suprotnom (slika 2, d).

U općem slučaju i izračunavaju se pomoću formula

, (12)

gdje je , nelinearna funkcija (karakteristika nelinearnog elementa).

Uzimajući u obzir gore navedeno, pri proučavanju samooscilacija bliskih harmoničkim, nelinearni ASR (Sl. 3) zamjenjuje se ekvivalentnim s harmoničkim koeficijentom linearizacije umjesto nelinearnog elementa (Sl. 5). Izlazni signal nelinearnog elementa na Sl. 5 je označen kao , ovo je

naglašava da nelinearni element generira samo

prvi harmonik oscilacija. Formule za harmonijske koeficijente linearizacije za tipične nelinearnosti mogu se naći u literaturi, na primjer, u. Tablica B u dodatku prikazuje karakteristike relejnih elemenata koji se proučavaju, formule i njihove hodografe. Formule i hodografi za inverzni harmonijski koeficijent linearizacije definiran izrazom

, (13)

gdje su i stvarni i imaginarni dijelovi. Hodografi i konstruirani su u koordinatama , odnosno .

Zapišimo sada uvjete postojanja autooscilacija. Sustav na Sl. 5 je ekvivalentan linearnom. U linearnom sustavu postoje neprigušene oscilacije ako je on na granici stabilnosti. Iskoristimo uvjet granice stabilnosti prema Nyquistovom kriteriju:

. (14)

jednadžba (14) Tamo je uvjet za postojanje samooscilacija, blizu harmonijskom. Ako postoje stvarno pozitivno rješenja A i w 0 jednadžbe (14), tada u nelinearnom ASR postoje samooscilacije bliske harmoničkim. Inače, samooscilacije su odsutne ili nisu harmonične. Jednadžba (14) se dijeli na dva dijela – s obzirom na realni i imaginarni dio:

;

Dijeleći obje strane jednadžbe (14) i uzimajući u obzir formulu (13), dobivamo uvjet postojanja samooscilacija u obliku L.S. Goldfarba:

. (17)

Jednadžba (17) također se dijeli na dvije:

(18)

a u nekim je slučajevima prikladnije koristiti ih za određivanje parametara vlastitih oscilacija.

Goldfarb je predložio grafičko-analitičku metodu za rješavanje sustava (17) i određivanje stabilnosti vlastitih oscilacija.

U koordinatama , i , konstruirani su hodografi i (slika 6, a). Ako se hodografi sijeku, tada postoje samooscilacije. U sjecištima se određuju parametri vlastitih oscilacija - A i w 0 - frekvencija w 0 prema hodografu, amplituda prema hodografu. Na sl. 6,a – dvije točke presjeka, što ukazuje na postojanje dva granična ciklusa.

Za određivanje stabilnosti samooscilacija, prema Goldfarbu, lijeva strana AFC-a linearnog dijela je osjenčana kada se kreće duž AFC-a u smjeru povećanja frekvencije (slika 6).

Autooscilacije su stabilne ako u točki sjecišta hodograf nelinearnog elementa prelazi iz nezasjenjenog područja u zasjenjeno područje kada se kreće u smjeru povećanja amplitude A.

Ako se dogodi prijelaz iz zasjenjenog područja u nezasjenjeno područje, tada autooscilacije nisu stabilne.

Na sl. Slika 6b kvalitativno prikazuje fazni portret koji odgovara dvama graničnim ciklusima na slici. 6, a. Točka sjecišta s parametrima i na sl. 6a odgovara nestabilnom graničnom ciklusu na sl. 6b, točka s parametrima i i za postizanje poremećaja vlastitih oscilacija, u ovom slučaju hodografa i ne sijeku se. Isti se učinak može postići povećanjem mrtve zone d ili smanjenjem amplitude izlaznog signala releja B. Postoji određena granična vrijednost K l pri kojoj AFC linearnog dijela dodiruje Greška! Greška u komunikaciji. pri čemu , a vrijednost amplitude je . Naravno, to dovodi do kvalitativne promjene u faznom portretu sustava.

Blizina vlastitih oscilacija harmoničkim omogućuje nam korištenje metode harmonijske linearizacije za određivanje njihovih parametara - amplitude A i frekvencije w 0. Metoda se temelji na pretpostavci da je linearni dio sustava niskopropusni filtar (hipoteza filtra). Odredimo uvjete pod kojima samooscilacije u sustavu mogu biti bliske harmoničkim. Ograničimo se na sustave koji, kao na Sl. 3 može se svesti na serijski spoj nelinearnog elementa i linearnog dijela. Pretpostavimo da je referentni signal konstantna vrijednost, radi jednostavnosti, uzet ćemo ga jednak nuli. A signal greške (slika 3) je harmoničan:

Izlazni signal nelinearnog elementa, kao i svaki periodički signal - na slici 3 su to pravokutne oscilacije - može se prikazati kao zbroj harmonika Fourierovog reda.

Dakle, ako je linearni dio sustava niskopropusni filtar, a frekvencija samooscilacija w 0 zadovoljava uvjete

, (4)

barem dva

Uvjet (6) je zadovoljen za mnoge realne sustave. Primjer je aperiodična veza drugog reda i realna integracija

gdje su i gdje su stvarni i imaginarni dijelovi,

– argument,

– modul.

brojčano je jednaka omjeru amplitude prvog harmonika na izlazu nelinearnog elementa i amplitude ulaznog harmoničkog signala.

Argument

karakterizira fazni pomak između prvog harmonika izlaznih oscilacija i ulaznog harmonijskog signala. Za nedvosmislene nelinearnosti, kao što je, na primjer, na Sl. 2,a i 2,b, realni izraz i

Za dvosmislene nelinearnosti, Sl. 2,c, 2,d, određeno formulom

gdje je S područje petlje histereze. Područje S uzima se s predznakom plus ako se petlja histereze zaobilazi u pozitivnom smjeru (slika 2, c) i s predznakom minus u suprotnom (slika 2, d).

U općem slučaju i izračunavaju se pomoću formula

gdje je , nelinearna funkcija (karakteristika nelinearnog elementa).

Naglašava da nelinearni element samo generira

gdje su i stvarni i imaginarni dijelovi. Hodografi i konstruirani su u koordinatama , odnosno .

Zapišimo sada uvjete postojanja autooscilacija. Sustav na Sl. 5 je ekvivalentan linearnom. U linearnom sustavu postoje neprigušene oscilacije ako je on na granici stabilnosti. Poslužimo se uvjetom granice stabilnosti prema Nyquistovom kriteriju: . Na sl. 6,a – dvije točke presjeka, što ukazuje na postojanje dva granična ciklusa.

Metoda harmonijske linearizacije omogućuje proučavanje stabilnosti i točnosti nelinearnih sustava s dovoljnom točnošću za praksu, korištenjem metoda razvijenih za linearne sustave. Metoda omogućuje određivanje prisutnosti vlastitih oscilacija, kao i njihove frekvencije i amplitude.

Nelinearni sustav se prikazuje kao veza linearnih i nelinearnih dijelova (slika 5).

Riža. 5 Dijagram nelinearnog sustava

Izlazni signal nelinearnog dijela sustava općenito je određen izrazom

Označimo kao prijenosnu funkciju linearnog dijela. Sustav jednadžbi poprimit će oblik

Nađimo uvjete pod kojima na izlazu linearnog dijela sustava nastaju harmonijske oscilacije oblika

U ovom slučaju signal y(t) predstavljat će i nelinearni dio periodična funkcija, ali se razlikuje od sinusoide. Ova se funkcija može proširiti u Fourierov red

U ovom izrazu a i I b i- Fourierovi koeficijenti. Za simetrične nelinearnosti F 0 =0.

Glavni uvjet koji metoda nameće linearnom dijelu sustava je uvjet niskopropusnog filtra. Vjeruje se da linearni dio prenosi samo prvi harmonik oscilacija. Ova pretpostavka nam omogućuje da više harmonike u (7.19) smatramo nevažnima i da se ograničimo na razmatranje samo prvog harmonika signala y(t).

tada se izraz (7.20) može prepisati kao

Prva jednadžba sustava (7.17) imat će oblik

U ovom izrazu

Rezultat zamjene nelinearnosti F(x,sx) izraz

a naziva se harmonijska linearizacija. Količine q I q 1 nazivaju se harmonijski linearizacijski koeficijenti ili jednostavno harmonijski koeficijenti. Za jednovrijedne nelinearnosti obično je q 1 =0 . Formule za harmoničke koeficijente koji odgovaraju tipičnim nelinearnostima dane su u prilozima.

Temeljna razlika između harmonijske linearizacije i konvencionalne linearizacije je u tome što se kod konvencionalne linearizacije nelinearna karakteristika zamjenjuje ravnom linijom s određenim konstantnim nagibom, a kod harmonijske linearizacije - ravnom linijom, čiji nagib ovisi o amplitudi ulaza signal nelinearnog elementa.

Razmotrimo tehniku određivanja amplitude i frekvencije vlastitih oscilacija.

1). U karakterističnoj jednadžbi sustava dobivenoj iz (7.22) vršimo zamjenu s=j i dobivamo

2). Iz dobivenog izraza izdvajamo realni i imaginarni dio i izjednačavamo ih s nulom, što prema Mihajlovljevom kriteriju odgovara da se sustav nalazi na granici oscilatorne stabilnosti.

3). Rješavanjem ovog sustava dobivaju se frekvencije i vrijednosti harmonijskih koeficijenata. Ako su te vrijednosti stvarne i pozitivne, tada sustav ima granični ciklus. Iz vrijednosti harmonijskih koeficijenata može se odrediti amplituda graničnog ciklusa.
4). Opće obilježje stabilnosti graničnog ciklusa, tj. postojanje autooscilacija je jednakost nuli pretposljednje Hurwitzeve determinante pri dobivenim vrijednostima amplitude i frekvencije graničnog ciklusa. Često je prikladnije koristiti uvjet stabilnosti graničnog ciklusa, koji se temelji na Mihajlovljevom kriteriju stabilnosti.

Ako je ova nejednakost zadovoljena, tada je granični ciklus stabilan iu sustavu postoje samooscilacije s gore definiranom amplitudom i frekvencijom. Indeks “*” znači da su derivati izračunati kada poznate vrijednosti harmonijski koeficijenti, amplituda i frekvencija.

Primjer. Pretpostavimo da je u sustavu stabilizacije kuta nagiba zrakoplova koji je već razmatran gore, upravljački pogon nelinearan i njegov strukturni dijagram ima oblik prikazan na Sl. 7.6.

sl.6 Nelinearni upravljački pogonski krug

Postavimo sljedeće parametre za nelinearnost brzinskih karakteristika kormilarskog pogona: b = 0,12, k 1 = tg =c/b = 6,7. Koeficijenti harmonijske linearizacije ove nelinearnosti određeni su izrazima

Zamjenom nelinearne karakteristike u krugu harmonijskim koeficijentom dobivamo prijenosnu funkciju pogona upravljača

Zamijenimo ovu prijenosnu funkciju u blok dijagram sustava stabilizacije kuta nagiba i odredimo prijenosnu funkciju zatvoreni sustav

U karakterističnoj jednadžbi zatvorenog sustava vršimo zamjenu s = j te izdvojiti stvarne i imaginarne dijelove.

Iz druge jednadžbe sustava dobivamo izraz za frekvenciju: , a zamjenom u prvu jednadžbu nakon transformacija dobivamo

Zamjenom ovdje prethodno definiranih izraza za koeficijente karakteristične jednadžbe možemo dobiti kvadratnu jednadžbu za harmonijski koeficijent čijim rješavanjem nalazimo

Pomoću ovih vrijednosti možete za dva slučaja izračunati sve koeficijente karakteristične jednadžbe i odrediti frekvencije koje odgovaraju svakoj vrijednosti q(A). Dobivamo:

Obje vrijednosti harmonijskog koeficijenta i odgovarajuće frekvencije su stvarne i pozitivne. Posljedično, postoje dva granična ciklusa u sustavu. Vrijednosti amplitude graničnog ciklusa određuju se numerički odabirom vrijednosti pri kojoj formula za harmonijski koeficijent linearizacije daje vrijednost jednaku prethodno izračunatoj. U slučaju koji razmatramo dobivamo

Procijenimo sada stabilnost graničnih ciklusa. Koristimo nejednakost dobivenu iz Mihajlovljevog kriterija, za koju definiramo

Derivacija koeficijenta harmonijske linearizacije uključena u dobivene izraze izračunava se pomoću formule

Izračuni pomoću gornjih formula pokazuju da prvi granični ciklus nije stabilan i javlja se kada (0) 0.1166(6.7 0 ). Ako je početno odstupanje manje od navedenog, tada se proces na ulazu nelinearnog elementa prigušuje (slika 7. 7) i sustav je stabilan.

Ako je početna vrijednost kuta nagiba veća od zadane, tada procesi konvergiraju u drugi granični ciklus, koji je stabilan i stoga u sustavu nastaju samooscilacije (slika 8).

Riža. 8

Modeliranjem je utvrđeno da područje privlačenja stabilnog graničnog ciklusa leži približno unutar granica (0) 0.1167 - 1.4 (6.71 0 - 80.2 0 ).

samarapedsovet.ru