Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.
Пусть дано линейное пространство R n и действующий в нем линейный оператор A; в этом случае оператор A переводит R n в себя, то есть A:R n → R n .

Определение. Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов оператора A, отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы оператора A с попарно различными собственными числами λ 1 , λ 2 , …, λ m линейно независимы.
3. Если собственные числа λ 1 =λ 2 = λ m = λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов , соответствующих различным собственным числам λ 1 , λ 2 , …, λ n , то они линейно независимы, следовательно, их можно принять за базис пространства R n . Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса - собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов Пусть дан вектор , где x 1 , x 2 , …, x n - координаты вектора x относительно базиса и x - собственный вектор линейного оператора A, соответствующий собственному числу λ , то есть . Это соотношение можно записать в матричной форме

. (*)

Уравнение (*) можно рассматривать как уравнение для отыскания x , причем , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда det(A - λE) = 0. Таким образом, для того, чтобы λ было собственным числом оператора A необходимо и достаточно, чтобы det(A - λE) = 0.
Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)
где - матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

Получили уравнение для нахождения собственных чисел.
Это уравнение называется характеристическим уравнением, а его левая часть - характеристическим многочленом матрицы (оператора) A. Если характеристический многочлен не имеет вещественных корней, то матрица A не имеет собственных векторов и ее нельзя привести к диагональному виду.
Пусть λ 1 , λ 2 , …, λ n - вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример 12. Линейный оператор A действует в R 3 по закону , где x 1 , x 2 , .., x n - координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
.
Составляем систему для определения координат собственных векторов:

Составляем характеристическое уравнение и решаем его:

.
λ 1,2 = -1, λ 3 = 3.
Подставляя λ = -1 в систему, имеем:
или
Так как , то зависимых переменных два, а свободное одно.
Пусть x 1 - свободное неизвестное, тогда Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как n - r = 3 - 2 = 1.
Множество собственных векторов, отвечающих собственному числу λ = -1, имеет вид: , где x 1 - любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x 1 = 1: .
Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу λ = 3: .
В пространстве R 3 базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в R 3 составить нельзя. Следовательно, матрицу A линейного оператора привести к диагональному виду не можем.

Пример 13. Дана матрица .
1. Доказать, что вектор является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.
Решение.
1. Если , то x - собственный вектор

.
Вектор (1, 8, -1) - собственный вектор. Собственное число λ = -1.
Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.
Собственные векторы ищем из системы:

Характеристическое уравнение: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Найдем собственный вектор, отвечающий собственному числу λ = -3:

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение x 1 = x 3 = 0. x 2 здесь может быть любым, отличным от нуля, например, x 2 = 1. Таким образом, вектор (0,1,0) является собственным вектором, отвечающим λ = -3. Проверим:
.
Если λ = 1, то получаем систему
Ранг матрицы равен двум. Последнее уравнение вычеркиваем.
Пусть x 3 - свободное неизвестное. Тогда x 1 = -3x 3 , 4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3 , x 2 = -9x 3 .
Полагая x 3 = 1, имеем (-3,-9,1) - собственный вектор, отвечающий собственному числу λ = 1. Проверка:

.
Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в R 3 . Таким образом, в базисе , , матрица A имеет вид:
.
Не всякую матрицу линейного оператора A:R n → R n можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше n. Однако, если матрица симметрическая, то корню характеристического уравнения кратности m соответствует ровно m линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .
Замечания. 1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.
В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

www.сайт позволяет найти . Сайт производит вычисление . За неколько секунд сервер выдаст правильное решение. Характеристическим уравнение для матрицы будет являться алгебраическое выражение, найденное по правилу вычисления определителя матрицы матрицы , при этом по главной диагонали будут стоять разницы значений диагональных элементов и переменной. При вычислении характеристического уравнения для матрицы онлайн , каждый элемент матрицы будет перемножаться с соответствующими другими элементами матрицы . Найти в режиме онлайн можно только для квадратной матрицы . Операция нахождения характеристического уравнения для матрицы онлайн сводится к вычислению алгебраической суммы произведения элементов матрицы как результат от нахождения определителя матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Данная операция занимает особое место в теории матриц , позволяет найти собственные числа и векторы, используя корни . Задача по нахождению характеристического уравнения для матрицы онлайн заключается в перемножении элементов матрицы с последующим суммированием этих произведений по определенному правилу. www.сайт находит характеристическое уравнение для матрицы заданной размерности в режиме онлайн . Вычисление характеристического уравнения для матрицы онлайн при заданной её размерности - это нахождение многочлена с числовыми или символьными коэффициентами, найденного по правилу вычисления определителя матрицы - как сумма произведений соответствующих элементов матрицы , только с целью определения характеристического уравнения для матрицы онлайн . Нахождение полинома относительно переменной для квадратной матрицы , как определение характеристического уравнения для матрицы , распространено в теории матриц . Значение корней многочлена характеристического уравнения для матрицы онлайн используется для определения собственных векторов и собственных чисел для матрицы . При этом, если определитель матрицы будет равен нулю, то характеристическое уравнение матрицы все равно будет существовать, в отличии от обратной матрицы . Для того, чтобы вычислить характеристическое уравнение для матрицы или найти сразу для нескольких матриц характеристические уравнения , необходимо затратить не мало времени и усилий, в то время как наш сервер в считанные секунды найдет характеристическое уравнение для матрицы онлайн . При этом ответ по нахождению характеристического уравнения для матрицы онлайн будет правильным и с достаточной точностью, даже если числа при нахождении характеристического уравнения для матрицы онлайн будут иррациональными. На сайте www.сайт допускаются символьные записи в элементах матриц , то есть характеристическое уравнение для матрицы онлайн может быть представлено в общем символьном виде при вычислении характеристического уравнения матрицы онлайн . Полезно проверить ответ, полученный при решении задачи по нахождению характеристического уравнения для матрицы онлайн , используя сайт www.сайт . При совершении операции вычисления полинома - характеристического уравнения матрицы , необходимо быть внимательным и предельно сосредоточенным при решении данной задачи. В свою очередь наш сайт поможет Вам проверить своё решение на тему характеристическое уравнение матрицы онлайн . Если у Вас нет времени на долгие проверки решенных задач, то www.сайт безусловно будет являться удобным инструментом для проверки при нахождении и вычислении характеристического уравнения для матрицы онлайн .

". В первой части изложены положения, минимально необходимые для понимания хемометрики, а во второй части - факты, которые необходимо знать для более глубокого постижения методов многомерного анализа. Изложение иллюстрируется примерами, выполненными в рабочей книге Excel Matrix.xls , которая сопровождает этот документ.

Ссылки на примеры помещены в текст как объекты Excel. Эти примеры имеют абстрактный характер, они никак не привязаны к задачам аналитической химии. Реальные примеры использования матричной алгебры в хемометрике рассмотрены в других текстах, посвященных разнообразным хемометрическим приложениям.

Большинство измерений, проводимых в аналитической химии, являются не прямыми, а косвенными . Это означает, что в эксперименте вместо значения искомого аналита C (концентрации) получается другая величина x (сигнал), связанная, но не равная C, т.е. x (C) ≠ С. Как правило, вид зависимости x (C) не известен, однако, к счастью, в аналитической химии большинство измерений пропорциональны. Это означает, что при увеличении концентрации С в a раз, сигнал X увеличится на столько же., т.е. x (a C) = a x (C). Кроме того, сигналы еще и аддитивны, так что сигнал от пробы, в которой присутствуют два вещества с концентрациями C 1 и C 2 , будет равен сумме сигналов от каждого компонента, т.е. x (C 1 + C 2) = x (C 1)+ x (C 2). Пропорциональность и аддитивность вместе дают линейность . Можно привести много примеров, иллюстрирующих принцип линейности, но достаточно упомянуть два самых ярких примера - хроматографию и спектроскопию. Вторая особенность, присущая эксперименту в аналитической химии - это многоканальность . Современное аналитическое оборудование одновременно измеряет сигналы для многих каналов. Например, измеряется интенсивность пропускания света сразу для нескольких длин волн, т.е. спектр. Поэтому в эксперименте мы имеем дело со множеством сигналов x 1 , x 2 ,...., x n , характеризующих набор концентраций C 1 ,C 2 , ..., C m веществ, присутствующих в изучаемой системе.

Рис. 1 Спектры

Итак, аналитический эксперимент характеризуется линейностью и многомерностью. Поэтому удобно рассматривать экспериментальные данные как векторы и матрицы и манипулировать с ними, используя аппарат матричной алгебры. Плодотворность такого подхода иллюстрирует пример, показанный на , где представлены три спектра, снятые для 200 длин волн от 4000 до 4796 cm −1 . Первый (x 1) и второй (x 2) спектры получены для стандартных образцов, в которых концентрация двух веществ A и B, известны: в первом образце [A] = 0.5, [B] = 0.1, а во втором образце [A] = 0.2, [B] = 0.6. Что можно сказать о новом, неизвестном образце, спектр которого обозначен x 3 ?

Рассмотрим три экспериментальных спектра x 1 , x 2 и x 3 как три вектора размерности 200. Средствами линейной алгебры можно легко показать, что x 3 = 0.1 x 1 +0.3 x 2 , поэтому в третьем образце очевидно присутствуют только вещества A и B в концентрациях [A] = 0.5×0.1 + 0.2×0.3 = 0.11 и [B] = 0.1×0.1 + 0.6×0.3 = 0.19.

1. Базовые сведения 1.1 Матрицы

Матрицей называется прямоугольная таблица чисел, например

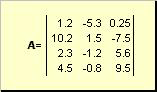
Рис. 2 Матрица

Матрицы обозначаются заглавными полужирными буквами (A ), а их элементы - соответствующими строчными буквами с индексами, т.е. a ij . Первый индекс нумерует строки, а второй - столбцы. В хемометрике принято обозначать максимальное значение индекса той же буквой, что и сам индекс, но заглавной. Поэтому матрицу A можно также записать как { a ij , i = 1,..., I ; j = 1,..., J }. Для приведенной в примере матрицы I = 4, J = 3 и a 23 = −7.5.

Пара чисел I и J называется размерностью матрицы и обознается как I ×J . Примером матрицы в хемометрике может служить набор спектров, полученный для I образцов на J длинах волн.

1.2. Простейшие операции с матрицами

Матрицы можно умножать на числа . При этом каждый элемент умножается на это число. Например -

Рис. 3 Умножение матрицы на число

Две матрицы одинаковой размерности можно поэлементно складывать и вычитать . Например,

Рис. 4 Сложение матриц

В результате умножения на число и сложения получается матрица той же размерности.

Нулевой матрицей называется матрица, состоящая из нулей. Она обозначается O . Очевидно, что A +O = A , A −A = O и 0A = O .

Матрицу можно транспонировать . При этой операции матрица переворачивается, т.е. строки и столбцы меняются местами. Транспонирование обозначается штрихом, A " или индексом A t . Таким образом, если A = {a ij , i = 1,..., I ; j = 1,...,J }, то A t = {a ji , j = 1,...,J ; i = 1,..., I }. Например

Рис. 5 Транспонирование матрицы

Очевидно, что (A t) t = A , (A +B ) t = A t +B t .

1.3. Умножение матриц

Матрицы можно перемножать , но только в том случае, когда они имеют соответствующие размерности. Почему это так, будет ясно из определения. Произведением матрицы A , размерностью I ×K , и матрицы B , размерностью K ×J , называется матрица C , размерностью I ×J , элементами которой являются числа

Таким образом для произведения AB необходимо, чтобы число столбцов в левой матрице A было равно числу строк в правой матрице B . Пример произведения матриц -

Рис.6 Произведение матриц

Правило перемножения матриц можно сформулировать так. Для того, чтобы найти элемент матрицы C , стоящий на пересечении i -ой строки и j -ого столбца (c ij ) надо поэлементно перемножить i -ую строку первой матрицы A на j -ый столбец второй матрицы B и сложить все результаты. Так в показанном примере, элемент из третьей строки и второго столбца, получается как сумма поэлементных произведений третьей строки A и второго столбца B

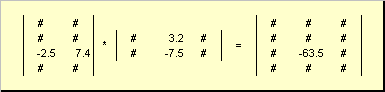
Рис.7 Элемент произведения матриц

Произведение матриц зависит от порядка, т.е. AB ≠ BA , хотя бы по соображениям размерности. Говорят, что оно некоммутативно. Однако произведение матриц ассоциативно. Это означает, что ABC = (AB )C = A (BC ). Кроме того, оно еще и дистрибутивно, т.е. A (B +C ) = AB +AC . Очевидно, что AO = O .

1.4. Квадратные матрицы

Если число столбцов матрицы равно числу ее строк (I = J = N ), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

Единичной матрицей (обозначается I, а иногда E ) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

Очевидно AI = IA = A .

Матрица называется диагональной , если все ее элементы, кроме диагональных (a ii ) равны нулю. Например

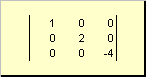
Рис. 8 Диагональная матрица

Матрица A называется верхней треугольной , если все ее элементы, лежащие ниже диагонали, равны нулю, т.е. a ij = 0, при i >j . Например

Рис. 9 Верхняя треугольная матрица

Аналогично определяется и нижняя треугольная матрица.

Матрица A называется симметричной , если A t = A . Иными словами a ij = a ji . Например

Рис. 10 Симметричная матрица

Матрица A называется ортогональной , если

A t A = AA t = I .

Матрица называется нормальной если

1.5. След и определитель

Следом квадратной матрицы A (обозначается Tr(A ) или Sp(A )) называется сумма ее диагональных элементов,

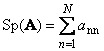
Например,

Рис. 11 След матрицы

Очевидно, что

Sp(α A ) = α Sp(A ) и

Sp(A +B ) = Sp(A )+ Sp(B ).

Можно показать, что

Sp(A ) = Sp(A t), Sp(I ) = N ,

а также, что

Sp(AB ) = Sp(BA ).

Другой важной характеристикой квадратной матрицы является ее определитель (обозначается det(A )). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта - матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

В случае матрицы (N ×N ) определитель вычисляется как сумма 1·2·3· ... ·N = N ! слагаемых, каждый из которых равен

Индексы k 1 , k 2 ,..., k N определяются как всевозможные упорядоченные перестановки r чисел в наборе (1, 2, ... , N ). Вычисление определителя матрицы - это сложная процедура, которую на практике осуществляется с помощью специальных программ. Например,

Рис. 12 Определитель матрицы

Отметим только очевидные свойства:

det(I ) = 1, det(A ) = det(A t),

det(AB ) = det(A )det(B ).

1.6. Векторы

Если матрица состоит только из одного столбца (J = 1), то такой объект называется вектором . Точнее говоря, вектором-столбцом. Например

Можно рассматривать и матрицы, состоящие из одной строки, например

Этот объект также является вектором, но вектором-строкой . При анализе данных важно понимать, с какими векторами мы имеем дело - со столбцами или строками. Так спектр, снятый для одного образца можно рассматривать как вектор-строку. Тогда набор спектральных интенсивностей на какой-то длине волны для всех образцов нужно трактовать как вектор-столбец.

Размерностью вектора называется число его элементов.

Ясно, что всякий вектор-столбец можно превратить в вектор-строку транспонированием, т.е.

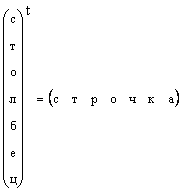
В тех случаях, когда форма вектора специально не оговаривается, а просто говорится вектор, то имеют в виду вектор-столбец. Мы тоже будем придерживаться этого правила. Вектор обозначается строчной прямой полужирной буквой. Нулевым вектором называется вектор, все элементы которого раны нулю. Он обозначается 0 .

1.7. Простейшие операции с векторами

Векторы можно складывать и умножать на числа так же, как это делается с матрицами. Например,

Рис. 13 Операции с векторами

Два вектора x и y называются колинеарными , если существует такое число α, что

1.8. Произведения векторов

Два вектора одинаковой размерности N можно перемножить. Пусть имеются два вектора x = (x 1 , x 2 ,...,x N) t и y = (y 1 , y 2 ,..., y N) t . Руководствуясь правилом перемножения "строка на столбец", мы можем составить из них два произведения: x t y и xy t . Первое произведение

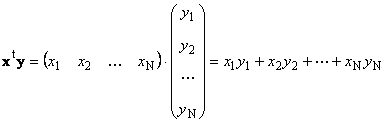
называется скалярным или внутренним . Его результат - это число. Для него также используется обозначение (x ,y )= x t y . Например,

Рис. 14 Внутреннее (скалярное) произведение

Второе произведение

называется внешним . Его результат - это матрица размерности (N ×N ). Например,

Рис. 15 Внешнее произведение

Векторы, скалярное произведение которых равно нулю, называются ортогональными .

1.9. Норма вектора

Скалярное произведение вектора самого на себя называется скалярным квадратом. Эта величина

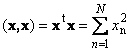
определяет квадрат длины вектора x . Для обозначения длины (называемой также нормой вектора) используется обозначение

Например,

Рис. 16 Норма вектора

Вектор единичной длины (||x || = 1) называется нормированным. Ненулевой вектор (x ≠ 0 ) можно нормировать, разделив его на длину, т.е. x = ||x || (x/ ||x ||) = ||x || e . Здесь e = x/ ||x || - нормированный вектор.

Векторы называются ортонормированными, если все они нормированы и попарно ортогональны.

1.10. Угол между векторами

Скалярное произведение определяет и угол φ между двумя векторами x и y

Если вектора ортогональны, то cosφ = 0 и φ = π/2, а если они колинеарны, то cosφ = 1 и φ = 0.

1.11. Векторное представление матрицы

Каждую матрицу A размера I ×J можно представить как набор векторов

Здесь каждый вектор a j является j -ым столбцом, а вектор-строка b i является i -ой строкой матрицы A

1.12. Линейно зависимые векторы

Векторы одинаковой размерности (N ) можно складывать и умножать на число, также как матрицы. В результате получится вектор той же размерности. Пусть имеется несколько векторов одной размерности x 1 , x 2 ,...,x K и столько же чисел α α 1 , α 2 ,...,α K . Вектор

y = α 1 x 1 + α 2 x 2 +...+ α K x K

называется линейной комбинацией векторов x k .

Если существуют такие ненулевые числа α k ≠ 0, k = 1,..., K , что y = 0 , то такой набор векторов x k называется линейно зависимым . В противном случае векторы называются линейно независимыми. Например, векторы x 1 = (2, 2) t и x 2 = (−1, −1) t линейно зависимы, т.к. x 1 +2x 2 = 0

1.13. Ранг матрицы

Рассмотрим набор из K векторов x 1 , x 2 ,...,x K размерности N . Рангом этой системы векторов называется максимальное число линейно-независимых векторов. Например в наборе

имеются только два линейно независимых вектора, например x 1 и x 2 , поэтому ее ранг равен 2.

Очевидно, что если векторов в наборе больше, чем их размерность (K >N ), то они обязательно линейно зависимы.

Рангом матрицы (обозначается rank(A )) называется ранг системы векторов, из которых она состоит. Хотя любую матрицу можно представить двумя способами (векторы столбцы или строки), это не влияет на величину ранга, т.к.

1.14. Обратная матрица

Квадратная матрица A называется невырожденной, если она имеет единственную обратную матрицу A -1 , определяемую условиями

AA −1 = A −1 A = I .

Обратная матрица существует не для всех матриц. Необходимым и достаточным условием невырожденности является

det(A ) ≠ 0 или rank(A ) = N .

Обращение матрицы - это сложная процедура, для выполнения которой существуют специальные программы. Например,

Рис. 17 Обращение матрицы

Приведем формулы для простейшего случая - матрицы 2×2

Если матрицы A и B невырождены, то

(AB ) −1 = B −1 A −1 .

1.15. Псевдообратная матрица

Если матрица A вырождена и обратная матрица не существует, то в некоторых случаях можно использовать псевдообратную матрицу, которая определяется как такая матрица A + , что

AA + A = A .

Псевдобратная матрица - не единственная и ее вид зависит от способа построения. Например для прямоугольной матрицы можно использовать метод Мура-Пенроуза .

Если число столбцов меньше числа строк, то

A + =(A t A ) −1 A t

Например,

Рис. 17a Псевдообращение матрицы

Если же число столбцов больше числа строк, то

A + =A t (AA t) −1

1.16. Умножение вектора на матрицу

Вектор x можно умножать на матрицу A подходящей размерности. При этом вектор-столбец умножается справа Ax , а вектор строка - слева x t A . Если размерность вектора J , а размерность матрицы I ×J то в результате получится вектор размерности I . Например,

Рис. 18 Умножение вектора на матрицу

Если матрица A - квадратная (I ×I ), то вектор y = Ax имеет ту же размерность, что и x . Очевидно, что

A (α 1 x 1 + α 2 x 2) = α 1 Ax 1 + α 2 Ax 2 .

Поэтому матрицы можно рассматривать как линейные преобразования векторов. В частности Ix = x , Ox = 0 .

2. Дополнительная информация 2.1. Системы линейных уравнений

Пусть A - матрица размером I ×J , а b - вектор размерности J . Рассмотрим уравнение

Ax = b

относительно вектора x , размерности I . По сути - это система из I линейных уравнений с J неизвестными x 1 ,...,x J . Решение существует в том, и только в том случае, когда

rank(A ) = rank(B ) = R ,

где B - это расширенная матрица размерности I ×(J+1 ), состоящая из матрицы A , дополненной столбцом b , B = (A b ). В противном случае уравнения несовместны.

Если R = I = J , то решение единственно

x = A −1 b .

Если R < I , то существует множество различных решений, которые можно выразить через линейную комбинацию J −R векторов. Система однородных уравнений Ax = 0 с квадратной матрицей A (N ×N ) имеет нетривиальное решение (x ≠ 0 ) тогда и только тогда, когда det(A ) = 0. Если R = rank(A ) 0.

Аналогично определяются отрицательно (x t Ax < 0), неотрицательно (x t Ax ≥ 0) и неположительно (x t Ax ≤ 0) определенные матрицы.

2.4. Разложение Холецкого

Если симметричная матрица A положительно определена, то существует единственная треугольная матрица U с положительными элементами, для которой

A = U t U .

Например,

Рис. 19 Разложение Холецкого

2.5. Полярное разложение

Пусть A - это невырожденная квадратная матрица размерности N ×N . Тогда существует однозначное полярное представление

A = SR,

где S - это неотрицательная симметричная матрица, а R - это ортогональная матрица. Матрицы S и R могут быть определены явно:

S 2 = AA t или S = (AA t) ½ и R = S −1 A = (AA t) −½ A .

Например,

Рис. 20 Полярное разложение

Если матрица A вырождена, то разложение не единственно - а именно: S по-прежнему одна, а вот R может быть много. Полярное разложение представляет матрицу A как комбинацию сжатия/растяжения S и поворота R .

2.6. Собственные векторы и собственные значения

Пусть A - это квадратная матрица. Вектор v называется собственным вектором матрицы A , если

Av = λv ,

где число λ называется собственным значением матрицы A . Таким образом преобразование, которое выполняет матрица A над вектором v , сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если v - собственный вектор, то и αv - тоже собственный вектор.

2.7. Собственные значения

У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных значений. Они удовлетворяют характеристическому уравнению

det(A − λI ) = 0,

являющемуся алгебраическим уравнением N -го порядка. В частности, для матрицы 2×2 характеристическое уравнение имеет вид

Например,

Рис. 21 Собственные значения

Набор собственных значений λ 1 ,..., λ N матрицы A называется спектром A .

Спектр обладает разнообразными свойствами. В частности

det(A ) = λ 1 ×...×λ N , Sp(A ) = λ 1 +...+λ N .

Собственные значения произвольной матрицы могут быть комплексными числами, однако если матрица симметричная (A t = A ), то ее собственные значения вещественны.

2.8. Собственные векторы

У матрицы A , размерностью (N ×N ) не может быть больше чем N собственных векторов, каждый из которых соответствует своему собственному значению. Для определения собственного вектора v n нужно решить систему однородных уравнений

(A − λ n I ) v n = 0 .

Она имеет нетривиальное решение, поскольку det(A − λ n I ) = 0.

Например,

Рис. 22 Собственные вектора

Собственные вектора симметричной матрицы ортогональны.

Инструкция

Число k называют собственным значением (числом) матрицы А, если существует вектор х , что Ax=kx. (1)При этом вектор х называется собственным вектором матрицы А, соответствующим числу k.В пространстве R^n (см. рис.1) матрица А имеет вид как на рисунке.

Необходимо поставить задачу нахождения и векторов матрицы А. Пусть собственный вектор x задан координатами. В матричной форме он запишется матрицей-столбцом, который для удобства следует представить транспонированной строкой. X=(x1,x2,…,xn)^T.Исходя из (1), Aх-kх=0 или Aх-kEх=0, где E – единичная матрица (единицы на главное диагонали, все остальное элементы – нули). Тогда (А-kE)х=0. (2)

Выражение (2) линейных однородных алгебраических уравнений, имеет ненулевое решение (собственный вектор). Поэтому главный определитель системы (2) равен нулю, то есть |А-kE|=0. (3) Последнее равенство собственного значения k называется характеристическим уравнением матрицы А и в развернутом виде имеет вид (см. рис.2).

Подставляя корень k характеристического уравнения в систему (2), однородную систему линейных уравнений с вырожденной матрицей (ее определитель равен нулю). Каждое ненулевое решение этой системы представляет собой собственный вектор матрицы А, соответствующий данному собственному числу k (то есть корню характеристического уравнения).

Пример. Найти собственные значения и векторы матрицы А (см. рис 3).Решение. Характеристическое уравнение представлено на рис. 3. Раскройте определитель и найдите собственные числа матрицы, которые являются данного уравнения (3-k)(-1-k)-5=0, (k-3)(k+1)-5=0, k^2-2k-8=0.Его корни k1=4, k2=-2

а) Собственные векторы, соответствующие k1=4, находятся, через решение системы (A-4kE)х=0. При этом требуется всего одно ее уравнение, так как определитель системы заведомо равен нулю. Если положить х=(x1, x2)^T, то первое уравнение системы (1-4)x1+x2=0, -3x1+x2=0. Если предположить, что х1=1 (только не ноль), то х2=3. Так как ненулевых решений у однородной системы с вырожденной матрицей сколь угодно много, то все множество собственных векторов, соответствующих первому собственному числу х =С1(1, 3), C1=const.

б) Найдите собственные векторы, соответствующие k2=-2. При решении системы (A+2kE)х=0, ее первое уравнение (3+2)х1+х2=0, 5х1+х2=0.Если положить х1=1, то х2=-5. Соответственные собственные векторы х =С2(1, 3), C2=const. Общее множество всех собственных векторов заданной матрицы: х =С1(1, 3)+ С2(1, 3).

Источники:

• Пискунов Н.С. Дифференциальное и интегральное исчисления. М., 1976, - 576 с.
• найти собственные числа и вектора матриц

Матрицы, представляющие собой табличную форму записи данных, широко применяются при работе с системами линейных уравнений. Причем число уравнений определяет количество строк матрицы, а количество переменных – порядок ее столбцов. В результате решение линейных систем сводится к операциям над матрицами, одна из которых – поиск собственных чисел матрицы. Их вычисление осуществляется с помощью характеристического уравнения. Собственные числа могут быть определены для квадратной матрицы порядка m.

Инструкция

Запишите заданную квадратную А. Для поиска ее собственных чисел используйте характеристическое уравнение, вытекающее из условия нетривиального решения линейной однородной системы, представленной в данном случае квадратной матрицей. Как следует из Крамера, решение существует только в том случае, если ее определитель равен нулю. Таким образом, можно записать уравнение | A - λE | = 0, где А – заданная , λ – искомые числа, E – единичная матрица, у которой все элементы на главной диагонали равны единице, а остальные – нулю.

Выполните умножение искомой переменной λ на единичную матрицу Е той же размерности, что и заданная исходная А. Результатом операции будет являться матрица, где по главной диагонали расположены значения λ, остальные элементы остаются равными нулю.

Как вставить математические формулы на сайт?

Если нужно когда-никогда добавлять одну-две математические формулы на веб-страницу, то проще всего сделать это, как описано в статье : математические формулы легко вставляются на сайт в виде картинок, которые автоматически генерирует Вольфрам Альфа. Кроме простоты, этот универсальный способ поможет улучшить видимость сайта в поисковых системах. Он работает давно (и, думаю, будет работать вечно), но морально уже устарел.

Если же вы постоянно используете математические формулы на своем сайте, то я рекомендую вам использовать MathJax - специальную библиотеку JavaScript, которая отображает математические обозначения в веб-браузерах с использованием разметки MathML, LaTeX или ASCIIMathML.

Есть два способа, как начать использовать MathJax: (1) при помощи простого кода можно быстро подключить к вашему сайту скрипт MathJax, который будет в нужный момент автоматически подгружаться с удаленного сервера (список серверов ); (2) закачать скрипт MathJax с удаленного сервера на свой сервер и подключить ко всем страницам своего сайта. Второй способ - более более сложный и долгий - позволит ускорить загрузку страниц вашего сайта, и если родительский сервер MathJax по каким-то причинам станет временно недоступен, это никак не повлияет на ваш собственный сайт. Несмотря на эти преимущества, я выбрал первый способ, как более простой, быстрый и не требующий технических навыков. Следуйте моему примеру, и уже через 5 минут вы сможете использовать все возможности MathJax на своем сайте.

Подключить скрипт библиотеки MathJax с удаленного сервера можно при помощи двух вариантов кода, взятого на главном сайте MathJax или же на странице документации :

Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.

Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.

Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией.

Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера.